Hostname: page-component-f554764f5-44mx8 Total loading time: 0 Render date: 2025-04-17T18:34:37.487Z Has data issue: false hasContentIssue false
  • English
  • Français

ON PROVING CONSISTENCY OF EQUATIONAL THEORIES IN BOUNDED ARITHMETIC

Part of: Proof theory and constructive mathematics Computability and recursion theory

Published online by Cambridge University Press:  27 January 2025

ARNOLD BECKMANN Open the ORCID record for ARNOLD BECKMANN [Opens in a new window]  and
YORIYUKI YAMAGATA Open the ORCID record for YORIYUKI YAMAGATA [Opens in a new window]
ARNOLD BECKMANN*
Affiliation:
DEPARTMENT OF COMPUTER SCIENCE SWANSEA UNIVERSITY SWANSEA SA2 8PP, UK
YORIYUKI YAMAGATA
Affiliation:
GRADUATE SCHOOL OF ENGINEERING UNIVERSITY OF FUKUI 3-9-1 BUNKYO FUKUI CITY, FUKUI JAPAN E-mail: [email protected]
*
E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider equational theories based on axioms for recursively defining functions, with rules for equality and substitution, but no form of induction—we denote such equational theories as PETS for pure equational theories with substitution. An example is Cook’s system PV without its rule for induction. We show that the Bounded Arithmetic theory 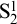$\mathrm {S}^{1}_2$ proves the consistency of PETS. Our approach employs model-theoretic constructions for PETS based on approximate values resembling notions from domain theory in Bounded Arithmetic, which may be of independent interest.

Keywords

Bounded Arithmeticequational theoriesseparation problem

MSC classification

Primary: 03F30: First-order arithmetic and fragments
Secondary: 03D15: Complexity of computation (including implicit computational complexity)
Type
Article
Information
The Journal of Symbolic Logic , Volume 90 , Issue 1 , March 2025 , pp. 135 - 165
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Beckmann, A., Proving consistency of equational theories in bounded arithmetic . Journal of Symbolic Logic , vol. 67 (2002), no. 1, pp. 279–296.CrossRefGoogle Scholar
Buss, S. R., Bounded Arithmetic , Bibliopolis, Naples, 1986. Revision of 1985 Princeton University Ph.D. thesis.Google Scholar
Samuel, R., Relating the bounded arithmetic and polynomial-time hierarchies . Annals of Pure and Applied Logic , vol. 75 (1995), pp. 67–77.Google Scholar
Buss, S. R. and Ignjatovic, A., Unprovability of consistency statements in fragments of bounded arithmetic . Annals of Pure Applied Logic , vol. 74 (1995), no. 3, pp. 221–244.CrossRefGoogle Scholar
Cook, S. A., Feasibly constructive proofs and the propositional calculus , Proceedings of the Seventh Annual ACM Symposium on Theory of Computing , 1975, pp. 83–97.CrossRefGoogle Scholar
Krajíček, J., Bounded Arithmetic, Propositional Calculus and Complexity Theory , Cambridge University Press, Heidelberg, 1995.CrossRefGoogle Scholar
Krajiček, J., Pudlák, P., and Takeuti, G., Bounded arithmetic and the polynomial hierarchy . Annals of Pure and Applied Logic , vol. 52 (1991), pp. 143–153.CrossRefGoogle Scholar
Pudlák, P., A note on bounded arithmetic . Fundamenta Mathematicae , vol. 136 (1990), no. 2, pp. 85–89.CrossRefGoogle Scholar
Vickers, S., Topology via Logic , Cambridge University Press, Cambridge, 1996.Google Scholar
Yamagata, Y., Consistency proof of a fragment of PA with substitution in bounded arithmetic . The Journal of Symbolic Logic , vol. 83 (2018), no. 3, pp. 1063–1090.CrossRefGoogle Scholar
Zambella, D., Notes on polynomially bounded arithmetic . Journal of Symbolic Logic , vol. 61 (1996), pp. 942–966.CrossRefGoogle Scholar