On large cardinals and partition relations

Extract

A significant portion of the study of large cardinals in set theory centers around the concept of “partition relation”. To best capture the basic idea here, we introduce the following notation: for x and y sets, κ an infinite cardinal, and γ an ordinal less than κ, we let [x]^γ denote the collection of subsets of x of order-type γ and abbreviate with 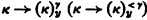the partition relation for each function F from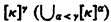into y there exists a subset C of κ of cardinality κ such that (such that for each α < γ) the range of F on [С]^γ ([С]^α) has cardinality 1. Now although each infinite cardinal κ satisfies the relation 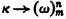for each n and m in ω (F. P. Ramsey [8]), a connection with large cardinals arises when one asks, “For which uncountable κ do we have κ → (κ)²?” Indeed, any uncountable cardinal κ which satisfies κ → (κ)² is strongly inaccessible and weakly compact (see [9]). As another example one can look at the improvements of Scott's original result to the effect that if there exists a measurable cardinal then there exists a nonconstructible set. Indeed, if κ is a measurable cardinal then κ → (κ)^{< ω}, and as Solovay [11] has shown, if there exists a cardinal κ such that κ → (κ)^{< ω3} (κ → (ℵ₁)^{< ω}, even) then there exists a nonconstructible set of integers.