Article contents
On a result of Szemerédi
Published online by Cambridge University Press: 12 March 2014
Abstract
We provide a short proof that if κ is a regular cardinal with κ < c, then
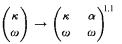
for any ordinal α < min{ , κ}. In particular,
, κ}. In particular,
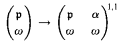
for any ordinal α <  . This generalizes an unpublished result of E. Szemerédi that Martin's axiom implies that
. This generalizes an unpublished result of E. Szemerédi that Martin's axiom implies that
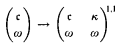
for any cardinal κ with κ < c.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2008
References
REFERENCES
- 3
- Cited by


