Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Арсланов, Марат Мирзаевич
and
Arslanov, Marat Mirzaevich
2011.
Теоретико-модельные свойства тьюринговых степеней разностной иерархии Ершова.
Современные проблемы математики,
Vol. 15,
Issue. ,
p.
5.
Arslanov, M. M.
2012.
Model-theoretic properties of the n-c.e. degrees.
Journal of Logic and Computation,
Vol. 22,
Issue. 4,
p.
669.
Arslanov, M. M.
2012.
Model-theoretic properties of turing degrees in the Ershov difference hierarchy.
Proceedings of the Steklov Institute of Mathematics,
Vol. 278,
Issue. S1,
p.
57.
CAI, MINGZHONG
SHORE, RICHARD A.
and
SLAMAN, THEODORE A.
2012.
THE n-r.e. DEGREES: UNDECIDABILITY AND Σ1 SUBSTRUCTURES.
Journal of Mathematical Logic,
Vol. 12,
Issue. 01,
p.
1250005.
Lempp, S.
2014.
A survey of results on the d.c.e. and n-c.e. degrees.
Lobachevskii Journal of Mathematics,
Vol. 35,
Issue. 4,
p.
313.
Liu, Yong
2019.
Isolated maximal d.r.e. degrees.
Annals of Pure and Applied Logic,
Vol. 170,
Issue. 4,
p.
515.
Liu, Yong
and
Peng, Cheng
2020.
Weak Density and Nondensity among Transfinite Levels of the Ershov Hierarchy.
Notre Dame Journal of Formal Logic,
Vol. 61,
Issue. 4,
Yamaleev, M. M.
2020.
Isolation from Side in 2-Computably Enumerable Degrees.
Russian Mathematics,
Vol. 64,
Issue. 8,
p.
70.
Arslanov, M. M.
and
Yamaleev, M. M.
2021.
Turing Computability: Structural Theory.
Journal of Mathematical Sciences,
Vol. 256,
Issue. 1,
p.
1.
Yamaleev, M. M.
2023.
Isolation from Side and Cone Avoidance in the 2-Computably Enumerable wtt-Degrees.
Journal of Mathematical Sciences,
Vol. 275,
Issue. 1,
p.
54.


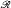 of recursively enumerable degrees is not a Σ
of recursively enumerable degrees is not a Σ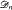 , where
, where 