No CrossRef data available.
Article contents
A note on transfinite iteration
Published online by Cambridge University Press: 12 March 2014
Extract
For some of the well-known set-theoretic operations a natural definition of transfinite iterations (powers) seems impossible. If, however, an operator D has the property that, for every X, D(X) ⊃ X, we may write the formula Dn(X) = D(Dn−1(X)) (which defines as usual the finite powers of D) in the form 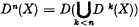 . Assuming this formula to be valid when n is any ordinal, we obtain a natural definition of transfinite powers of those operators. Obviously the dual definition would work in the case D(X) ⊂ X.
. Assuming this formula to be valid when n is any ordinal, we obtain a natural definition of transfinite powers of those operators. Obviously the dual definition would work in the case D(X) ⊂ X.
As an example of the use of this definition, we show how the sets used by von Neumann to represent ordinals can be constructed by means of the operator N(X) = X⋃{X}. Denoting the union of the elements of X by S(X), we have for the set E(ξ), which represents the ordinal ξ, E(ξ) = S(Nξ({ϕ})), as can easily be verified by transfinite induction. As the sets E(ξ) are different for different values of ξ, the powers of N are all different as well.
This is not always the case. The powers of certain operators start repeating themselves from a certain ordinal onward. If an operator has the property that, for every set A of sets a, 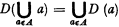 , then the sequence of its powers becomes constant already from ω on. This is a special case of the following theorem.
, then the sequence of its powers becomes constant already from ω on. This is a special case of the following theorem.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1956
References
1 von Neumann, J., Zur Einführung der transfiniten Zahlen, Acta Szeged, vol. 1 (1933), pp. 199–208Google Scholar.
2 Mostowski, A., Über die Unabhängigkeit des Wohlordnungssatzes vom Ordnungsprinzip, Fundamenta mathematicae, vol. 32 (1939), pp. 201–252CrossRefGoogle Scholar.
3 As I was informed by Prof. Mostowski, the same possibility of simplification was noticed by P. Bernays.


