Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-02-07T01:49:16.274Z Has data issue: false hasContentIssue false
  • English
  • Français

NON-TIGHTNESS IN CLASS THEORY AND SECOND-ORDER ARITHMETIC

Part of: Nonstandard models Model theory Set theory

Published online by Cambridge University Press:  13 June 2023

ALFREDO ROQUE FREIRE Open the ORCID record for ALFREDO ROQUE FREIRE [Opens in a new window]  and
KAMERYN J. WILLIAMS
ALFREDO ROQUE FREIRE
Affiliation:
CENTER FOR RESEARCH AND DEVELOPMENT IN MATHEMATICS AND APPLICATIONS—CIDMA UNIVERSITY OF AVEIRO, CAMPUS UNIVERSITÁRIO DE SANTIAGO 3810-193 AVEIRO, PORTUGAL E-mail: [email protected]
KAMERYN J. WILLIAMS*
Affiliation:
DIVISION OF SCIENCE, MATHEMATICS, AND COMPUTING BARD COLLEGE AT SIMON’S ROCK, 84 ALFORD ROAD GREAT BARRINGTON, MA 01230, USA URL: http://kamerynjw.net
*
E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

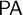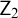A theory T is tight if different deductively closed extensions of T (in the same language) cannot be bi-interpretable. Many well-studied foundational theories are tight, including $\mathsf {PA}$ [39], $\mathsf {ZF}$, $\mathsf {Z}_2$, and 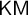$\mathsf {KM}$ [6]. In this article we extend Enayat’s investigations to subsystems of these latter two theories. We prove that restricting the Comprehension schema of 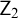$\mathsf {Z}_2$ and 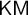$\mathsf {KM}$ gives non-tight theories. Specifically, we show that $\mathsf {GB}$ and $\mathsf {ACA}_0$ each admit different bi-interpretable extensions, and the same holds for their extensions by adding 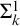$\Sigma ^1_k$-Comprehension, for 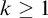$k \ge 1$. These results provide evidence that tightness characterizes 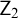$\mathsf {Z}_2$ and 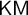$\mathsf {KM}$ in a minimal way.

Keywords

class theoryinterpretationssecond-order arithmetictightness

MSC classification

Primary: 03C62: Models of arithmetic and set theory 03E70: Nonclassical and second-order set theories 03H15: Nonstandard models of arithmetic
Type
Article
Information
The Journal of Symbolic Logic , First View , pp. 1 - 28
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Antos, C. and Friedman, S.-D., Hyperclass forcing in Morse–Kelley class theory, this Journal, vol. 82 (2017), no. 2, pp. 549–575.Google Scholar
Antos, C. and Gitman, V., Modern class forcing , Research Trends in Contemporary Logic (Daghighi, A., Rezus, A., Pourmahdian, M., Gabbay, D., and Fitting, M., editors), College Publications (Forthcoming). Available at https://philarchive.org/archive/ANTMCFv1.Google Scholar
Button, T. and Walsh, S., Structure and categoricity: Determinacy of reference and truth value in the philosophy of mathematics . Philosophia Mathematica , vol. 24 (2016), no. 3, pp. 283–307.CrossRefGoogle Scholar
Dedekind, R., Was sind und was sollen die Zahlen?, Was sind und was sollen die Zahlen? Stetigkeit und Irrationale Zahlen , Vieweg + Teubner, Wiesbaden, 1965, pp. 1–47.CrossRefGoogle Scholar
Dodd, A., The Core Model , London Mathematical Society Lecture Note Series, vol. 61, Cambridge University Press, Cambridge, 1982.CrossRefGoogle Scholar
Enayat, A., Variations on a Visserian theme , Liber Amicorum Alberti: A Tribute to Albert Visser (van Eijck, J., Iemhoff, R., and Joosten, J. J., editors), College Publications, London, 2016, pp. 99–110.Google Scholar
Enayat, A., Tightness, solidity, and internal categoricity, in preparation.Google Scholar
Feferman, S., Arithmetization of metamathematics in a general setting . Fundamenta Mathematicae , vol. 49 (1960), no. 1, pp. 35–92.CrossRefGoogle Scholar
Feferman, S., Transfinite recursive progressions of axiomatic theories, this Journal, vol. 27 (1962), no. 3, pp. 259–316.Google Scholar
Feferman, S., Some applications of forcing and generic sets . Fundamenta Mathematica , vol. 56 (1965), pp. 325–345.CrossRefGoogle Scholar
Feferman, S., Kreisel, G., and Orey, S., 1—Consistency and faithful interpretations . Archiv für Mathematische Logik und Grundlagenforschung , vol. 6 (1962), no. 1, pp. 52–63.CrossRefGoogle Scholar
Freire, A. R.. Irreducible features of set theories, in review, 2021. doi:10.13140/RG.2.2.20667.44322/1.CrossRefGoogle Scholar
Freire, A. R. and Hamkins, J. D., Bi-interpretation in weak set theories, this Journal, vol. 86 (2020), no. 2, 609–634.Google Scholar
Friedman, S. D., Fine Structure and Class Forcing (Reprint 2011 Edition) , De Gruyter Series in Logic and Its Applications, vol. 3, De Gruyter, Berlin, 2000.Google Scholar
Gitman, V. and Hamkins, J. D., Open determinacy for class games , Foundations of Mathematics, Logic at Harvard, Essays in Honor of Hugh Woodin’s 60th Birthday (Caicedo, A. E., Cummings, J., Koellner, P., and Larson, P.), Contemporary Mathematics, American Mathematical Society, Providence, 2017. Available at http://jdh.hamkins.org/open-determinacy-for-class-games.Google Scholar
Gitman, V., Hamkins, J. D., Holy, P., Schlicht, P., and Williams, K. J., The exact strength of the class forcing theorem, this Journal, vol. 85 (2020), no. 3, 869–905.Google Scholar
Gitman, V., Hamkins, J. D., and Karagila, A., Kelley–Morse set theory does not prove the class Fodor theorem . Fundamenta Mathematicae , vol. 254 (2021), no. 2, pp. 133–154. Available at http://wp.me/p5M0LV-1RD.CrossRefGoogle Scholar
Hamkins, J. D., Different set theories are never bi-interpretable, 2018. Available at http://jdh.hamkins.org/different-set-theories-are-never-bi-interpretable/ (accessed 21 July, 2022).Google Scholar
Hamkins, J. D. and Seabold, D., Well-founded Boolean ultrapowers as large cardinal embeddings, 2006, pp. 1–40. Available at http://jdh.hamkins.org/boolean-ultrapowers/.Google Scholar
Hamkins, J. D. and Woodin, W. H., Open class determinacy is preserved by forcing, 2018, under review, pp. 1–14. Available at http://wp.me/p5M0LV-1KF.Google Scholar
Hodges, W., Model Theory , Cambridge University Press, Cambridge, 1993.CrossRefGoogle Scholar
Jensen, R. B., The fine structure of the constructible hierarchy . Annals of Mathematical Logic , vol. 4 (1972), no. 3, pp. 229–308.CrossRefGoogle Scholar
Jensen, R. B., Manuscript on fine structure, inner model theory, and the core model below one Woodin cardinal, Unpublished, 2021. Available at https://ivv5hpp.uni-muenster.de/u/rds/skript-2021-07-07.pdf.Google Scholar
Marek, W. and Mostowski, A., On extendability of models of ZF set theory to the models of Kelley–Morse theory of classes , ISILC Logic Conference: Proceedings of the International Summer Institute and Logic Colloquium, Kiel 1974 (Müller, G. H., Oberschelp, A., and Potthoff, K., editors), Springer, Berlin–Heidelberg, 1975, pp. 460–542.CrossRefGoogle Scholar
Mostowski, A., Some impredicative definitions in set theory . Fundamenta Mathematica , vol. 37 (1951), pp. 111–124.CrossRefGoogle Scholar
Odifreddi, P., Forcing and reducibilities, this Journal, vol. 48 (1983), no. 2, pp. 288–310.Google Scholar
Odifreddi, P., Forcing and reducibilities. II. Forcing in fragments of analysis, this Journal, vol. 48 (1983), no. 3, pp. 724–743.Google Scholar
Odifreddi, P., Forcing and reducibilities. III. Forcing in fragments of set theory, this Journal, vol. 48 (1983), no. 4, pp. 1013–1034.Google Scholar
Parsons, C., The structuralist view of mathematical objects . Synthese , vol. 84 (1990), no. 3, pp. 303–346.CrossRefGoogle Scholar
Putnam, H., Models and reality, this Journal, vol. 45 (1980), no. 3, pp. 464–482.Google Scholar
Ratajczyk, Z., On sentences provable in impredicative extensions of theories . Dissertationes Mathematicae , vol. 178 (1979), 1–44.Google Scholar
Scott, D., A different kind of model for set theory, unpublished paper, talk given at the 1960 Stanford Congress of Logic, Methodology, and Philosophy of Science, 1960.Google Scholar
Simpson, S. G., Subsystems of Second Order Arithmetic , Perspectives in Logic, Association for Symbolic Logic, New York, 2009.CrossRefGoogle Scholar
Stanley, M. C., A unique generic real , Ph.D. thesis, University of California at Berkeley, 1984.Google Scholar
Tarski, A., A general method in proofs of undecidability , Undecidable Theories , vol. 13 (Tarski, A., Mostowski, A., and Robinson, R. M., editors), Elsevier, Amsterdam, 1953, pp. 1–30.Google Scholar
Väänänen, J., Second order logic or set theory? . Bulletin of Symbolic Logic , vol. 18 (2012), no. 1, pp. 91–121.CrossRefGoogle Scholar
Väänänen, J., Tracing internal categoricity . Theoria , vol. 87 (2020), no. 4, pp. 986–1000.CrossRefGoogle Scholar
Väänänen, J. and Wang, T., Internal categoricity in arithmetic and set theory. Notre Dame Journal of Formal Logic , vol. 56 (2015), no. 1, pp. 121–134.CrossRefGoogle Scholar
Visser, A., Categories of theories and interpretations , Logic in Tehran , Lecture Notes in Logic, vol. 26, Association for Symbolic Logic, La Jolla, 2006, pp. 284–341.CrossRefGoogle Scholar
Williams, K. J., The structure of models of second-order set theory , Ph.D. thesis, The Graduate Center, CUNY, 2018.Google Scholar
Williams, K. J., Minimum models of second-order set theories, this Journal, vol. 84 (2019), no. 2, 589–620.Google Scholar
Zarach, A. M., Replacement $\nrightarrow$ collection , Gödel ’96: Logical Foundations of Mathematics, Computer Science and Physics—Kurt Gödel’s Legacy, Brno, Czech Republic, August 1996, Proceedings , vol. 6 , Lecture Notes in Logic, Springer, Berlin, 1996, pp. 307–322. Available at http://projecteuclid.org/euclid.lnl/1235417032.CrossRefGoogle Scholar
Zermelo, E., Über grenzzahlen und mengenbereiche: Neue untersuchungen über die grundlagen der mengenlehre . Fundamenta Mathematicae , vol. 16 (1930).CrossRefGoogle Scholar