Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T04:34:39.087Z Has data issue: false hasContentIssue false
  • English
  • Français

NIP FOR THE ASYMPTOTIC COUPLE OF THE FIELD OF LOGARITHMIC TRANSSERIES

Published online by Cambridge University Press:  21 March 2017

ALLEN GEHRET
ALLEN GEHRET*
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGN URBANA, IL 61801, USAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The derivation on the differential-valued field Tlog of logarithmic transseries induces on its value group 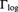${{\rm{\Gamma }}_{{\rm{log}}}}$ a certain map ψ. The structure 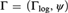${\rm{\Gamma }} = \left( {{{\rm{\Gamma }}_{{\rm{log}}}},\psi } \right)$ is a divisible asymptotic couple. In [7] we began a study of the first-order theory of 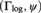$\left( {{{\rm{\Gamma }}_{{\rm{log}}}},\psi } \right)$ where, among other things, we proved that the theory 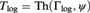$T_{{\rm{log}}} = Th\left( {{\rm{\Gamma }}_{{\rm{log}}} ,\psi } \right)$ has a universal axiomatization, is model complete and admits elimination of quantifiers (QE) in a natural first-order language. In that paper we posed the question whether Tlog has NIP (i.e., the Non-Independence Property). In this paper, we answer that question in the affirmative: Tlog does have NIP. Our method of proof relies on a complete survey of the 1-types of Tlog, which, in the presence of QE, is equivalent to a characterization of all simple extensions 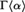${\rm{\Gamma }}\left\langle \alpha \right\rangle$ of ${\rm{\Gamma }}$. We also show that Tlog does not have the Steinitz exchange property and we weigh in on the relationship between models of Tlog and the so-called precontraction groups of [9].

Keywords

03C64asymptotic couplesasymptotic integrationlogarithmic transseriesindependence propertycontraction groups
Type
Articles
Information
The Journal of Symbolic Logic , Volume 82 , Issue 1 , March 2017 , pp. 35 - 61
Copyright
Copyright © The Association for Symbolic Logic 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adler, H., Introduction to theories without the independence property, http://www.logic.univie.ac.at/∼adler/docs/nip.pdf, June 2008.Google Scholar
Aschenbrenner, M., Some remarks about asymptotic couples , Valuation Theory and its Applications, vol. II (Saskatoon, SK, 1999) (Kuhlmann, F.-V., Kuhlmann, S., and Marshall, M., editors), Fields Institute Communications, vol. 33, American Mathematical Society, Providence, RI, 2003, pp. 7–18.Google Scholar
Aschenbrenner, M. and van den Dries, L., Closed asymptotic couples . Journal of Algebra, vol. 225 (2000), no. 1, pp. 309–358.CrossRefGoogle Scholar
Aschenbrenner, M., van den Dries, L., and van der Hoeven, J., Asymptotic differential algebra and model theory of transseries . Annals of Mathematics Studies, to appear, arXiv:1509.02588.Google Scholar
Belegradek, O., Peterzil, Y., and Wagner, F., Quasi-o-minimal structures, this Journal, vol. 65 (2000), no. 3, pp. 1115–1132.Google Scholar
Conway, J. H. and Guy, R. K., The Book of Numbers, Copernicus, New York, 1996.Google Scholar
Gehret, A., The asymptotic couple of the field of logarithmic transseries . Journal of Algebra, 2017, pp. 1–36. doi: 10.1016/j.jalgebra.2016.08.016.CrossRefGoogle Scholar
Jech, T., Set Theory, Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2003. The third millennium edition, revised and expanded.Google Scholar
Kuhlmann, F.-V., Abelian groups with contractions. I , Abelian Group Theory and Related Topics (Oberwolfach, 1993) (Göbel, R., Hill, P., and Liebert, W., editors), Contemporary Mathematics, vol. 171, American Mathematical Society, Providence, RI, 1994, pp. 217–241.Google Scholar
Kuhlmann, F.-V., Abelian groups with contractions. II. Weak o-minimality , Abelian Groups and Modules (Padova, 1994), Mathematics and its Applications, vol. 343, Kluwer Acadmic Publishers, Dordrecht, 1995, pp. 323–342.Google Scholar
Kuhlmann, S., Ordered Exponential Fields, Fields Institute Monographs, vol. 12, American Mathematical Society, Providence, RI, 2000.Google Scholar
Kunen, K., Set Theory, Studies in Logic and the Foundations of Mathematics, vol. 102, North-Holland, Amsterdam-New York, 1980. An introduction to independence proofs.Google Scholar
Marker, D., Model Theory, Graduate Texts in Mathematics, vol. 217, Springer-Verlag, New York, 2002. An introduction.Google Scholar
Miller, C., Tameness in expansions of the real field , Logic Colloquium ’01 (Baaz, M., Friedman, S.-D., and Krajíček, J., editors), Lecture Notes in Logic, vol. 20, Association for Symbolic Logic, Urbana, IL, 2005, pp. 281–316.Google Scholar
Mitchell, W., Aronszajn trees and the independence of the transfer property . Annals of Mathematical Logic, vol. 5 (1972/73), pp. 21–46.Google Scholar
Rosenlicht, M., On the value group of a differential valuation . American Journal of Mathematics, vol. 101 (1979), no. 1, pp. 258–266.Google Scholar
Rosenlicht, M., Differential valuations . Pacific Journal of Mathematics, vol. 86 (1980), no. 1, pp. 301–319.Google Scholar
Rosenlicht, M., On the value group of a differential valuation. II . American Journal of Mathematics, vol. 103 (1981), no. 5, pp. 977–996.Google Scholar
Shelah, S., Classification Theory and the Number of Nonisomorphic Models, second ed., Studies in Logic and the Foundations of Mathematics, vol. 92, North-Holland, Amsterdam, 1990.Google Scholar
Simon, P., A Guide to NIP Theories, Cambridge University Press, 2015.Google Scholar
Simon, P., Distal and non-distal NIP theories . Annals of Pure and Applied Logic, vol. 164 (2013), no. 3, pp. 294–318.Google Scholar