Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-02-11T15:28:32.762Z Has data issue: false hasContentIssue false
  • English
  • Français

Morley degree in unidimensional compact complex spaces

Published online by Cambridge University Press:  12 March 2014

Dale Radin
Dale Radin*
Affiliation:
Department of Mathematics, McMaster University, Hamilton, ON, L8S-4K1, Canada. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 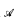be the category of all reduced compact complex spaces, viewed as a multi-sorted first order structure, in the standard way. Let 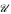be a sub-category of 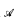. which is closed under the taking of products and analytic subsets, and whose morphisms include the projections. Under the assumption that Th(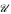) is unidimensional. we show that Morley rank is equal to Noetherian dimension, in any elementary extension of 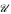. As a result, we are able to show that Morley degree is definable in Th(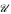). when Th(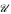) is unidimensional.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 71 , Issue 2 , June 2006 , pp. 569 - 585
Copyright
Copyright © Association for Symbolic Logic 2006

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Aroca, J.M., Hironaka, H., and Vicente, J.L., Desingularization theorems, Memorias de Matemática del Instituto Jorge Juan, Madrid, vol. 30 (1977).Google Scholar
[2]Grauert, H., Peternell, Th., and Remmert, R. (editors), Several complex variables VII, Encyclopedia of Mathematical Sciences, vol. 74, Springer-Verlag, 1994.CrossRefGoogle Scholar
[3]Grauert, H. and Remmert, R.. Coherent analytic sheaves, Grundlehren der Mathematischen Wissenschaften, vol. 265, Springer-Verlag, 1984.CrossRefGoogle Scholar
[4]Hrushovski, E.. Strongly minimal expansions of algebraically closed fields, Israel Journal of Mathematics, vol. 79 (1992), pp. 129–151.CrossRefGoogle Scholar
[5]Hrushovski, E. and Zilber, B.. Zariski geometries, Journal of the American Mathematical Society, vol. 9 (1996), no. 1, pp. 1–56.CrossRefGoogle Scholar
[6]Lascar, D., Stability in model theory, Pitman Monographs and Surveys in Pure and Applied Mathematics, vol. 36. Longman Scientific and Technical, 1987.Google Scholar
[7]Lieberman, D., Compactness of the Chow Scheme: Applications to automorphisms and deformations of Kähler manifolds, Seminaire F. Norguet, vol. 111. Lecture Notes in Mathematics, no. 670. Springer-Verlag. 1978.Google Scholar
[8]Moosa, R., Contributions to the model theory of fields and compact complex spaces, Ph.D. thesis. University of Illinois at Urbana-Champaign. 2001.Google Scholar
[9]Moosa, R., On saturation and the model theory of compact Kähler manifolds. To appear in the Journal für die reine und angewandte Mathematik, 2003.Google Scholar
[10]Moosa, R., The model theory of compact complex spaces. Logic colloquium '01 (Baaz, M.et al., editors), Lecture Notes in Logic, vol. 20. ASL and AK Peters, 2005, pp. 317–349.CrossRefGoogle Scholar
[11]Pillay, A., Some model theory of compact complex spaces, Workshop on Hubert's Tenth Problem: Relations with arithmetic and algebraic geometry, Contemporary Mathematics, vol. 270, American Mathematical Society, Providence, RI, 2000. pp. 323–338.Google Scholar
[12]Pillay, A. and Pong, W.Y.. On Lascar rank and Morley rank of definable groups in differentially closed fields, this Journal, vol. 67 (2002), pp. 1189–1196.Google Scholar
[13]Pillay, A. and Scanlon, T., Compact complex manifolds with the DOP and other properties, this Journal, vol. 67 (2002), pp. 737–743.Google Scholar
[14]Pillay, A. and Scanlon, T., Meronwrphic groups, Transactions of the AMS, vol. 355 (2003). no. 10, pp. 3843–3859.CrossRefGoogle Scholar
[15]Radin, D., A definability result for compact complex spaces, this Journal, vol. 691 (2004), no. 1. pp. 241–254.Google Scholar
[16]Radin, D., Unidimensional Zariski-type structures and applications to the model theory of compact complex spaces, Ph.D. thesis, University of Illinois at Chicago, 2004.Google Scholar
[17]Shelah, S.. Classification theory (revised edition), Studies in Logic and the Foundations of Mathematics, vol. 92, North-Holland, 1990.Google Scholar
[18]Zilber, B., Lecture notes on Zariski-type structures. Delivered in the UIC logic seminar. Fall 1991.Google Scholar
[19]Zilber, B., Uncountably categorical theories. Translations of Mathematical Monographs, vol. 117. American Mathematical Society, 1993.CrossRefGoogle Scholar