Maximal irredundance and maximal ideal independence in Boolean algebras

Extract

Recall that a subset X of an algebra A is irredundant iff x ∉ 〈X∖{x}〉 for all x ϵ X, where 〈X∖{x}) is the subalgebra generated by X∖{x}. By Zorn's lemma there is always a maximal irredundant set in an algebra. This gives rise to a natural cardinal function Irr_mm(A) = min{∣X∣: X is a maximal irredundant subset of A}. The first half of this article is devoted to proving that there is an atomless Boolean algebra A of size 2^ω for which Irr_mm(A) = ω.

A subset X of a BA A is ideal independent iff x ∉ (X∖{x}〉^id for all x ϵ X, where 〈X∖{x}〉^id is the ideal generated by X∖{x}. Again, by Zorn's lemma there is always a maximal ideal independent subset of any Boolean algebra. We then consider two associated functions. A spectrum function

S_spect(A) = {∣X∣: X is a maximal ideal independent subset of A}

and the least element of this set, s_mm(A). We show that many sets of infinite cardinals can appear as S_spect(A). The relationship of S_mm to similar “continuum cardinals” is investigated. It is shown that it is relatively consistent that S_mm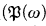/fin) < 2^ω.

We use the letter s here because of the relationship of ideal independence with the well-known cardinal invariant spread; see Monk [5]. Namely, sup{∣X∣: X is ideal independent in A} is the same as the spread of the Stone space Ult(A); the spread of a topological space X is the supremum of cardinalities of discrete subspaces.