Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T17:33:25.003Z Has data issue: false hasContentIssue false
  • English
  • Français

Mad Families Constructed from Perfect Almost Disjoint Families

Published online by Cambridge University Press:  12 March 2014

Jörg Brendle  and
Yurii Khomskii
Jörg Brendle
Affiliation:
Graduate School of System Informatics, Kobe University, Rokko-Dai 1-1, NADA, Kobe 657-8501, Japan, E-mail: [email protected]
Yurii Khomskii
Affiliation:
Kurt Gödel Research Center for Mathematical Logic, University of Vienna, Währinger Straße 25, 1090 Wien, Austria, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove the consistency of 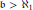together with the existence of a 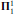-definable mad family, answering a question posed by Friedman and Zdomskyy in [7, Question 16]. For the proof we construct a mad family in L which is an ℵ1-union of perfect a.d. sets, such that this union remains mad in the iterated Hechler extension. The construction also leads us to isolate a new cardinal invariant, the Borel almost-disjointness number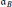, defined as the least number of Borel a.d. sets whose union is a mad family. Our proof yields the consistency of 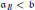(and hence, ).

Keywords

03E1503E1703E35Mad familiesprojective hierarchycardinal invariants
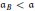Type
Research Article
Information
The Journal of Symbolic Logic , Volume 78 , Issue 4 , December 2013 , pp. 1164 - 1180
Copyright
Copyright © Association for Symbolic Logic 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Baumgartner, James E. and Dordal, Peter, Adjoining dominating functions, this Journal, vol. 50 (1985), no. 1, pp. 94–101.Google Scholar
[2] Brendle, Jörg, Forcing and the structure of the real line: the Bogotá lectures, Lecture notes, 2009.Google Scholar
[3] Brendle, Jörg, Aspects of iterated forcing, Tutorial at Winter School in Abstract Analysis, section Set Theory & Topology, 01/February 2010.Google Scholar
[4] Brendle, Jörg and Yatabe, Shunsuke, Forcing indestructibility of MAD families, Annals of Pure and Applied Logic, vol. 132 (2005), no. 2-3, pp. 271–312.Google Scholar
[5] Dow, Alan, Two classes of Fréchet-Urysohn spaces, Proceedings of the American Mathematical Society, vol. 108 (1990), no. 1, pp. 241–247.Google Scholar
[6] Fischer, Vera, Friedman, Sy David, and Zdomskyy, Lyubomyr, Projective wellorders and mad families with large continuum, Annals of Pure and Applied Logic, vol. 162 (2011), no. 11, pp. 853–862.Google Scholar
[7] Friedman, Sy-David and Zdomskyy, Lyubomyr, Projective mad families, Annals of Pure and Applied Logic, vol. 161 (2010), no. 12, pp. 1581–1587.Google Scholar
[8] Hrusak, Michael, MAD families and the rationals, Commentationes Mathematicae Universitatis Carolinae, vol. 42 (2001), no. 2, pp. 345–352.Google Scholar
[9] Kastermans, Bart, Steprāns, Juris, and Zhang, Yi, Analytic and coanalytic families of almost disjoint functions, this Journal, vol. 73 (2008), no. 4, pp. 1158–1172.Google Scholar
[10] Kurilić, Miloš S., Cohen-stable families of subsets of integers, this Journal, vol. 66 (2001), no. 1, pp. 257–270.Google Scholar
[11] Mathias, Adrian R. D., Happy families, Annals of Pure and Applied Logic, vol. 12 (1977), no. 1, pp. 59–111.Google Scholar
[12] Miller, Arnold W., Infinite combinatorics and definability, Annals of Pure and Applied Logic, vol. 41 (1989), no. 2, pp. 179–203.Google Scholar
[13] Raghavan, Dilip, Maximal almost disjoint families of functions, Fundamenta Mathematicae, vol. 204 (2009), no. 3, pp. 241–282.Google Scholar
[14] Raghavan, Dilip and Shelah, Saharon, Comparing the closed almost disjointness and dominating numbers, Fundamenta Mathematicae, vol. 217 (2012), pp. 73–81.Google Scholar
[15] Tòrnquist, Asger, Σ2 1 and Π1 1 mad families, this Journal, vol. 78 (2013), no. 4, pp. 1181–1182.Google Scholar