Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-18T15:30:07.114Z Has data issue: false hasContentIssue false
  • English
  • Français

A Limit Law of Almost l-partite Graphs

Published online by Cambridge University Press:  12 March 2014

Vera Koponen
Vera Koponen*
Affiliation:
Department of Mathematics, Uppsala University, Box 480, 75106 Uppsala, Sweden, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For integers l ≥ 1, d ≥ 0 we study (undirected) graphs with vertices 1, …, n such that the vertices can be partitioned into l parts such that every vertex has at most d neighbours in its own part. The set of all such graphs is denoted Pn (l, d). We prove a labelled first-order limit law, i.e., for every first-order sentence φ, the proportion of graphs in Pn (l, d) that satisfy φ converges as n → ∞. By combining this result with a result of Hundack, Prömel and Steger [12] we also prove that if 1 ≤ s1 ≤ … ≤ sl are integers, then Forb(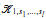) has a labelled first-order limit law, where Forb(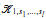) denotes the set of all graphs with vertices 1, …, n, for some n, in which there is no subgraph isomorphic to the complete (l + 1 )-partite graph with parts of sizes 1, s1, …, sl. In the course of doing this we also prove that there exists a first-order formula ξ, depending only on l and d, such that the proportion of ∈ Pn (l, d) with the following property approaches 1 as n → ∞: there is a unique partition of {1, …, n} into l parts such that every vertex has at most d neighbours in its own part, and this partition, viewed as an equivalence relation, is defined by ξ.

Keywords

Finite model theorylimit lawrandom graphforbidden subgraph
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 78 , Issue 3 , September 2013 , pp. 911 - 936
Copyright
Copyright © Association for Symbolic Logic 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Balogh, J., Bollobás, B., and Simonovits, M., The typical structure of graphs without given excluded subgraphs, Random Structures and Algorithms, vol. 34 (2009), pp. 305–318.CrossRefGoogle Scholar
[2] Balogh, J., Bollobás, B., and Simonovits, M., The fine structure of octahedron-free graphs, Journal of Combinatorial Theory, Series B, vol. 101 (2011), pp. 67–84.Google Scholar
[3] Burris, S. N., Number theoretic density and logical limit laws, Mathematical Surveys and Monographs, vol. 86, American Mathematical Society, 2001.Google Scholar
[4] Compton, K. J., A logical approach to asymptotic combinatorics. I. First order properties, Advances in Mathematics, vol. 65 (1987), pp. 65–96.Google Scholar
[5] Compton, K. J., The computational complexity of asymptotic problems I: Partial orders, Information and Computation, vol. 78 (1988), pp. 108–123.CrossRefGoogle Scholar
[6] Diestel, R., Graph theory, third ed., Springer, 2005.Google Scholar
[7] Ebbinghaus, H-D. and Flum, J., Finite model theory, second ed., Springer-Verlag, 1999.Google Scholar
[8] Erdős, P., Kleitman, D. J., and Rothschild, B. L., Asymptotic enumeration of Kn-free graphs, International Colloquium on Combinatorial Theory, vol. 2, Atti dei Convegni Lincei, no. 17, Rome, 1976, pp. 19–27.Google Scholar
[9] Fagin, R., Probabilities on finite models, this Journal, vol. 41 (1976), pp. 50–58.Google Scholar
[10] Glebskii, Y. V., Kogan, D. I., Liogonkii, M. I., and Talanov, V. A., Volume and fraction of satisfiability of formulas of the lower predicate calculus, Kibernetyka, vol. 2 (1969), pp. 17–27.Google Scholar
[11] Haber, S. and Krivelevich, M., The logic of random regular graphs, Journal of Combinatorics, vol. 1 (2010), pp. 389–440.Google Scholar
[12] Hundack, C., Prömel, H. J., and Steger, A., Extremal graph problems for graphs with a color-critical vertex, Combinatorics, Probability and Computing, vol. 2 (1993), pp. 465–477.Google Scholar
[13] Kolaitis, Ph. G., Prömel, H. J., and Rothschild, B. L., Kl+1-free graphs: asymptotic structure and a 0-1 law, Transactions of the American Mathematical Society, vol. 303 (1987), pp. 637–671.Google Scholar
[14] Koponen, V., Asymptotic probabilities of extension properties andrandom l-colourable structures, Annals of Pure and Applied Logic, vol. 163 (2012), pp. 391–438.Google Scholar
[15] Koponen, V., Random graphs with bounded maximum degree: asymptotic structure and a logical limit law, Discrete Mathematics and Theoretical Computer Science, vol. 14 (2012), pp. 229–254.Google Scholar
[16] Lynch, J. F., Convergence law for random graphs with specified degree sequence, ACM Transactions on Computational Logic, vol. 6 (2005), pp. 727–748.CrossRefGoogle Scholar
[17] Prömel, H. J. and Steger, A., The asymptotic number of graphs not containing a fixed color critical subgraph, Combinatorica, vol. 12 (1992), pp. 463–473.Google Scholar
[18] Shelah, S. and Spencer, J., Zero-one laws for sparse random graphs, Journal of the American Mathematical Society, vol. 1 (1988), pp. 97–115.Google Scholar
[19] Spencer, J., The strange logic of random graphs, Algorithms and Combinatorics, vol. 22, Springer-Verlag, 2001.Google Scholar