No CrossRef data available.
Article contents
LIFSCHITZ REALIZABILITY AS A TOPOLOGICAL CONSTRUCTION
Published online by Cambridge University Press: 08 January 2021
Abstract
We develop a number of variants of Lifschitz realizability for 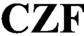 $\mathbf {CZF}$ by building topological models internally in certain realizability models. We use this to show some interesting metamathematical results about constructive set theory with variants of the lesser limited principle of omniscience including consistency with unique Church’s thesis, consistency with some Brouwerian principles and variants of the numerical existence property.
$\mathbf {CZF}$ by building topological models internally in certain realizability models. We use this to show some interesting metamathematical results about constructive set theory with variants of the lesser limited principle of omniscience including consistency with unique Church’s thesis, consistency with some Brouwerian principles and variants of the numerical existence property.
MSC classification
- Type
- Articles
- Information
- Copyright
- © The Association for Symbolic Logic 2021
References
REFERENCES
Aczel, P. and Rathjen, M., Notes on constructive set theory, Technical report 40, Institut Mittag-Leffler, 2001.Google Scholar
Aczel, P. and Rathjen, M., Notes on constructive set theory, Book draft available at http://www1.maths.leeds.ac.uk/~rathjen/book.pdf, 2010.Google Scholar
Akama, Y., Berardi, S., Hayashi, S., and Kohlenbach, U., An Arithmetical Hierarchy of the Law of Excluded Middle and Related Principles, Proceedings of the 19th Annual IEEE Symposium on Logic in Computer Science, 2004, Turku, Finland, July 2004, pp. 192–201.Google Scholar
Awodey, S. and Bauer, A., Propositions as [types]. Journal of Logic and Computation, vol. 14 (2004), no. 4, pp. 447–471.CrossRefGoogle Scholar
Chen, R.-M. and Rathjen, M., Lifschitz realizability for intuitionistic Zermelo-Fraenkel set theory. Archive for Mathematical Logic, vol. 51 (2012), no. 7–8, pp. 789–818 (English).CrossRefGoogle Scholar
Friedman, H., The consistency of classical set theory relative to a set theory with intuitionistic logic, this Journal, vol. 38 (1973), pp. 315–319.Google Scholar
Friedman, H., The disjunction property implies the numerical existence property. Proceedings of the National Academy of Sciences of the United States of America, vol. 72 (1975), no. 8, pp. 2877–2878.CrossRefGoogle ScholarPubMed
Gambino, N., Heyting-valued interpretations for constructive set theory. Annals of Pure and Applied Logic, vol. 137 (2006), no. 1–3, pp. 164–188.CrossRefGoogle Scholar
Hendtlass, M. and Lubarsky, R., Separating fragments of WLEM, LPO, and MP, this Journal, vol. 81 (2016), no. 4, pp. 1315–1343.Google Scholar
Koutsoulis, D.. Lifschitz realizability for homotopy type theory, Master’s thesis, Institute for Logic, Language and Computation, University of Amsterdam, 2019, Available at https://eprints.illc.uva.nl/1756/1/MoL-2019-26.text.pdf.Google Scholar
Lee, S. and van Oosten, J., Basic subtoposes of the effective topos. Annals of Pure and Applied Logic, vol. 164 (2013), no. 9, pp. 866–883.CrossRefGoogle Scholar
Lifschitz, V., CT0 is stronger than CT0!. Proceedings of the American Mathematical Society, vol. 73 (1979), no. 1, pp. 101–106.Google Scholar
Maietti, M. E., Modular correspondence between dependent type theories and categories including pretopoi and topoi. Mathematical Structures in Computer Science, vol. 15 (2005), pp. 1089–1149.Google Scholar
McCarty, D. C., Realizability and recursive mathematics, Ph.D. thesis, Ohio State University, 1984.Google Scholar
Rathjen, M., Constructive set theory and Brouwerian principles. Journal of Universal Computer Science, vol. 11 (2005), no. 12, pp. 2008–2033.Google Scholar
Rathjen, M., The disjunction and other properties for Constructive Zermelo-Frankel set theory, this Journal, vol. 70 (2005), pp. 1233–1254.Google Scholar
Rathjen, M., Constructive Zermelo-Fraenkel set theory and the limited principle of omniscience. Annals of Pure and Applied Logic, vol. 165 (2014), no. 2, pp. 563–572.CrossRefGoogle Scholar
Rathjen, M., Realizability for constructive Zermelo-Fraenkel set theory, Logic Colloquium ’03 (Stoltenberg-Hansen, V. and Väänänen, J., editors), Cambridge University Press, Cambridge, 2006, pp. 282–314.CrossRefGoogle Scholar
Richman, F., Polynomials and linear transformations. Linear Algebra and its Applications, vol. 131 (1990), pp. 131–137.CrossRefGoogle Scholar
van den Berg, B., The Herbrand topos. Mathematical Proceedings of the Cambridge Philosophical Society, vol. 155 (2013), no. 2, pp. 361–374.CrossRefGoogle Scholar
van Oosten, J., Lifschitz’ realizability, this Journal, vol. 55 (1990), no. 2, pp. 805–821.Google Scholar
van Oosten, J., Two remarks on the Lifschitz realizability topos, this Journal, vol. 61 (1996), no. 1, pp. 70–79.Google Scholar
van Oosten, J., Realizability: An Introduction to its Categorical Side, Studies in Logic and the Foundations of Mathematics, vol. 152, Elsevier, Amsterdam, 2008.Google Scholar



