Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-24T23:58:06.637Z Has data issue: false hasContentIssue false
  • English
  • Français

Leibnizian models of set theory

Published online by Cambridge University Press:  12 March 2014

Ali Enayat
Ali Enayat*
Affiliation:
Department of Mathematics and Statistics, American University, Washington, D.C., 20016-8050, USA, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract.

A model is said to be Leibnizian if it has no pair of indiscernibles. Mycielski has shown that there is a first order axiom LM (the Leibniz-Mycielski axiom) such that for any completion T of Zermelo-Fraenkel set theory ZF. T has a Leibnizian model if and only if T proves LM. Here we prove:

Theorem A. Every complete theory T extending ZF + LM has 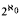nonisomorphic countable Leibnizian models.

Theorem B. If κ is a prescribed definable infinite cardinal ofa complete theory T extending ZF + V = OD, then there are 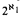nonisomorphic Leibnizian models 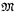of T of power ℵ1such that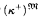is ℵ1-like.

Theorem C. Every complete theory T extendingZF + V = ODhas 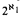nonisomorphic ℵ1-like Leibnizian models.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 69 , Issue 3 , September 2004 , pp. 775 - 789
Copyright
Copyright © Association for Symbolic Logic 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Abramson, and Harrington, L., Models without indiscernibles, this Journal, vol. 43 (1978), pp. 572–600.Google Scholar
[2]Chang, C. C. and Keisler, H. J., Model theory, Elsevier North Holland, Amsterdam, 1973.Google Scholar
[3]Cohen, P., Set theory and the continuum hypothesis, Benjamin, New York, 1966.Google Scholar
[4]Ehrenfeucht, A., Discernible elements in models of arithmetic, this Journal, vol. 38 (1973), pp. 291–292.Google Scholar
[5]Enayat, A., On certain elementary extensions of models of set theory, Transactions of the American Mathematical Society, vol. 283 (1984), pp. 705–715.CrossRefGoogle Scholar
[6]Enayat, A., Conservative extensions of models of set theory and generalizations, this Journal, vol. 51 (1986), pp. 1005–1021.Google Scholar
[7]Enayat, A., Power-like models of set theory, this Journal, vol. 66 (2001), pp. 1766–1782.Google Scholar
[8]Enayat, A., Counting models of set theory, Fundamenta Mathematicae, vol. 174 (2002), pp. 23–47.CrossRefGoogle Scholar
[9]Enayat, A., Models of set theory with definable ordinals, to appear in Archive for Mathematical Logic.Google Scholar
[10]Enayat, A., On the Leibniz-Mycielski axiom in set theory, to appear in Fundamenta Mathematicae.Google Scholar
[11]Enayat, A., Leibnizian models via iterated ultrapowers, in preparation.Google Scholar
[12]Jech, T., Set theory, Academic Press, New York, 1978.Google Scholar
[13]Keisler, H. J., Logic with the quantifier ”there exists uncountably many”, Annals of Mathematical Logic, vol. 1 (1970), pp. 1–94.CrossRefGoogle Scholar
[14]Knight, J., Hanf number for omitting types for particular theories, this Journal, vol. 41 (1976), pp. 583–588.Google Scholar
[15]Kossak, R. and Schmerl, J., Models of Arithmetic, monograph in preparation.Google Scholar
[16]Leibniz, G. W., Philosophical papers and letters, (Loemaker, L., translator and editor), second ed., D. Reidel, Dordecht, 1969.Google Scholar
[17]Mitchell, W., Aronszajn trees and the independence of the transfer property, Annals of Mathematical Logic, (1972), pp. 21–46.Google Scholar
[18]Mycielski, J., New set-theoretic axioms derived from a lean metamathematics, this Journal, vol. 60 (1995), pp. 191–198.Google Scholar
[19]Mycielski, J., Axioms which imply G.C.H., Fundamenta Mathematicae, vol. 176 (2003), pp. 193–207.CrossRefGoogle Scholar
[20]Myhill, J. and Scott, D., Ordinal definability, Axiomatic set theory, Part I, Proceedings of Symposia in Pure Mathematics, vol. 13, American Mathematical Society, Providence, R.I., 1970.Google Scholar
[21]Paris, J., Minimal models of ZF, Proceedings of the Bertrand Russell Memorial Logic Conference, Denmark 1973, Leeds, 1973.Google Scholar