No CrossRef data available.
Article contents
LEBESGUE MEASURE ZERO MODULO IDEALS ON THE NATURAL NUMBERS
Published online by Cambridge University Press: 29 December 2023
Abstract
We propose a reformulation of the ideal 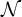 $\mathcal {N}$ of Lebesgue measure zero sets of reals modulo an ideal J on
$\mathcal {N}$ of Lebesgue measure zero sets of reals modulo an ideal J on 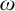 $\omega $, which we denote by
$\omega $, which we denote by 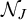 $\mathcal {N}_J$. In the same way, we reformulate the ideal
$\mathcal {N}_J$. In the same way, we reformulate the ideal 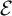 $\mathcal {E}$ generated by
$\mathcal {E}$ generated by 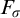 $F_\sigma $ measure zero sets of reals modulo J, which we denote by
$F_\sigma $ measure zero sets of reals modulo J, which we denote by 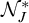 $\mathcal {N}^*_J$. We show that these are
$\mathcal {N}^*_J$. We show that these are 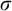 $\sigma $-ideals and that
$\sigma $-ideals and that 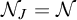 $\mathcal {N}_J=\mathcal {N}$ iff J has the Baire property, which in turn is equivalent to
$\mathcal {N}_J=\mathcal {N}$ iff J has the Baire property, which in turn is equivalent to 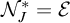 $\mathcal {N}^*_J=\mathcal {E}$. Moreover, we prove that
$\mathcal {N}^*_J=\mathcal {E}$. Moreover, we prove that 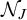 $\mathcal {N}_J$ does not contain co-meager sets and
$\mathcal {N}_J$ does not contain co-meager sets and 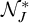 $\mathcal {N}^*_J$ contains non-meager sets when J does not have the Baire property. We also prove a deep connection between these ideals modulo J and the notion of nearly coherence of filters (or ideals).
$\mathcal {N}^*_J$ contains non-meager sets when J does not have the Baire property. We also prove a deep connection between these ideals modulo J and the notion of nearly coherence of filters (or ideals).
We also study the cardinal characteristics associated with 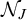 $\mathcal {N}_J$ and
$\mathcal {N}_J$ and 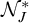 $\mathcal {N}^*_J$. We show their position with respect to Cichoń’s diagram and prove consistency results in connection with other very classical cardinal characteristics of the continuum, leaving just very few open questions. To achieve this, we discovered a new characterization of
$\mathcal {N}^*_J$. We show their position with respect to Cichoń’s diagram and prove consistency results in connection with other very classical cardinal characteristics of the continuum, leaving just very few open questions. To achieve this, we discovered a new characterization of 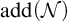 $\mathrm {add}(\mathcal {N})$ and
$\mathrm {add}(\mathcal {N})$ and 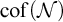 $\mathrm {cof}(\mathcal {N})$. We also show that, in Cohen model, we can obtain many different values to the cardinal characteristics associated with our new ideals.
$\mathrm {cof}(\mathcal {N})$. We also show that, in Cohen model, we can obtain many different values to the cardinal characteristics associated with our new ideals.
Keywords
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of The Association for Symbolic Logic



