Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-14T11:17:08.327Z Has data issue: false hasContentIssue false
  • English
  • Français

The largest countable inductive set is a mouse set

Published online by Cambridge University Press:  12 March 2014

Mitch Rudominer
Mitch Rudominer*
Affiliation:
Department of Mathematics, Florida International University, Miami. FL 33199, U.S.A. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let κℝ be the least ordinal κ such that Lκ (ℝ) is admissible. Let A = {x ϵ ℝ ∣ (∃α < κℝ) such that x is ordinal definable in Lα (ℝ)}. It is well known that (assuming determinacy) A is the largest countable inductive set of reals. Let T be the theory: ZFC − Replacement + “There exists ω Woodin cardinals which are cofinal in the ordinals.” T has consistency strength weaker than that of the theory ZFC + “There exists ω Woodin cardinals”, but stronger than that of the theory ZFC + “There exists n Woodin Cardinals”, for each n ϵ ω. Let M be the canonical, minimal inner model for the theory T. In this paper we show that A = ℝ ∩ M. Since M is a mouse, we say that A is a mouse set. As an application, we use our characterization of A to give an inner-model-theoretic proof of a theorem of Martin which states that for all n, every 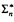real is in A.

Keywords

large cardinalsdescriptive set theoryinner model theory
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 64 , Issue 2 , June 1999 , pp. 443 - 459
Copyright
Copyright © Association for Symbolic Logic 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[Jech] Jech, Thomas, Set theory, Academic Press, Inc., San Diego, California, 1978.Google Scholar
[Kech] Kechris, A. S., The theory of countable analytical sets, Transactions of the American Mathematical Society, vol. 202 (1975), pp. 259–297.Google Scholar
[KeMaSo] Kechris, A. S., Martin, D. A., and Solovay, R. M., Introduction to Q-theory, Cabal seminar 79–81, vol. 1019, Springer-Verlag, 1983, pp. 199–281.Google Scholar
[Kunen] Kunen, Kenneth, Set theory: An introduction to independence proofs, Studies in Logic and the Foundations of Mathematics, vol. 102, North Holland, New York, N.Y., 1980.Google Scholar
[Ma1] Martin, D. A., untitled book on large cardinals and determinacy, In preparation.Google Scholar
[Ma2] Martin, D. A., The largest countable this, that, and the other, Cabal seminar 79–81, Lecture Notes in Mathematics, vol. 1019, Springer-Verlag, 1983, pp. 97–106.Google Scholar
[MiSt] Mitchell, W. J. and Steel, J. R., Fine structure and iteration trees, Lecture Notes in Logic, vol. 3, Springer-Verlag, 1994.CrossRefGoogle Scholar
[Mo] Moschovakis, Y. N., Descriptive set theory, North-Holland, 1980.Google Scholar
[Ru] Rudominer, M., Mouse sets, Annals of Pure and Applied Logic, vol. 87 (1997), pp. 1–100.CrossRefGoogle Scholar
[St1] Steel, J. R., Scales in L(ℝ), Cabal seminar 79–81, Lecture Notes in Mathematics, vol. 1019, Springer-Verlag, 1983, pp. 10–156.Google Scholar
[St2] Steel, J. R., Inner models with many Woodin cardinals, Annals of Pure and Applied Logic, vol. 65 (1993), pp. 185–209.Google Scholar
[St3] Steel, J. R., Projectively wellordered inner models, Annals of Pure and Applied Logic, vol. 74 (1995), pp. 77–104.Google Scholar
[St4] Steel, J. R., A theorem of Woodin's on mouse sets, Unpublished notes, 1996.Google Scholar