Article contents
Iterated reflection principles and the ω-rule
Published online by Cambridge University Press: 12 March 2014
Extract
The ω-rule,

with the meaning “if the formula A(n) is provable for all n, then the formula ∀xA(x) is provable”, has a certain formal similarity with a uniform reflection principle saying “if A(n) is provable for all n, then ∀xA(x) is true”. There are indeed some hints in the literature that uniform reflection has sometimes been understood as a “formalized ω-rule” (cf. for example S. Feferman [1], G. Kreisel [3], G. H. Müller [7]). This similarity has even another aspect: replacing the induction rule or scheme in Peano arithmetic PA by the ω-rule leads to a complete and sound system PA∞, where each true arithmetical statement is provable. In [2] Feferman showed that an equivalent system can be obtained by erecting on PA a transfinite progression of formal systems PAα based on iterations of the uniform reflection principle according to the following scheme:

Then T = (∪dЄ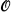 , PAd,
, PAd, 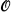 being Kleene's system of ordinal notations, is equivalent to PA∞. Of course, T cannot be an axiomatizable theory.
being Kleene's system of ordinal notations, is equivalent to PA∞. Of course, T cannot be an axiomatizable theory.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1982
References
REFERENCES
- 6
- Cited by


