Article contents
Innocuous substitutions
Published online by Cambridge University Press: 12 March 2014
Extract
In classical first-order predicate logic CL1 (without equality) only tautologies and antitautologies satisfy nontautological schemas. I.e., if F[p, Q] is a nontautological formula (fl) in the predicate letters shown, with p prepositional, then ⊬ F[K, Q] for any sentence K not containing some Q ∈ Q, unless ⊢ K or ⊢ ¬K. This is an easy consequence of the Completeness Theorem. Clearly, the analogous statement fails for intuitionistic predicate logic IL1; already when Q is empty: (i) 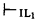 ¬¬ K for, e.g., K ≡ p ∨ ¬p; (ii)
¬¬ K for, e.g., K ≡ p ∨ ¬p; (ii) 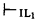 ¬¬K → K for, e.g., K ≡ ¬p.
¬¬K → K for, e.g., K ≡ ¬p.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1980
References
REFERENCES
- 1
- Cited by


