Article contents
Infinite substructure lattices of models of Peano Arithmetic
Published online by Cambridge University Press: 12 March 2014
Abstract
Bounded lattices (that is lattices that are both lower bounded and upper bounded) form a large class of lattices that include all distributive lattices, many nondistributive finite lattices such as the pentagon lattice N5. and all lattices in any variety generated by a finite bounded lattice. Extending a theorem of Paris for distributive lattices, we prove that if L is an ℵ0-algebraic bounded lattice, then every countable nonstandard model 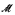 of Peano Arithmetic has a cofinal elementary extension
of Peano Arithmetic has a cofinal elementary extension 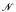 such that the interstructure lattice Lt(
such that the interstructure lattice Lt(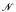 /
/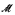 ) is isomorphic to L.
) is isomorphic to L.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2010
References
REFERENCES
- 2
- Cited by


