Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-28T04:25:56.181Z Has data issue: false hasContentIssue false
  • English
  • Français

Implicit proofs

Published online by Cambridge University Press:  12 March 2014

Jan Krajíček
Jan Krajíček*
Affiliation:
Mathematical Institute, Academy of Sciences, Žitná 25, Prague 1, CZ-115 67, The Czech Republic, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract.

We describe a general method how to construct from a prepositional proof system P a possibly much stronger proof system iP. The system iP operates with exponentially long P-proofs described “implicitly” by polynomial size circuits.

As an example we prove that proof system iEF, implicit EF, corresponds to bounded arithmetic theory 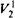and hence, in particular, polynomially simulates the quantified prepositional calculus G and the 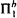-consequences of 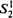proved with one use of exponentiation. Furthermore, the soundness of iEF is not provable in 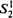. An iteration of the construction yields a proof system corresponding to T2 + Exp and, in principle, to much stronger theories.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 69 , Issue 2 , June 2004 , pp. 387 - 397
Copyright
Copyright © Association for Symbolic Logic 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Buss, S. R., Bounded arithmetic, Bibliopolis, Naples, 1986.Google Scholar
[2]Cook, S. A., Feasibly constructive proofs and the propositional calculus, Seventh Annual ACM Symposium on Theory of Computing, Association of Computing Machinery Press, 1975, pp. 83–97.CrossRefGoogle Scholar
[3]Cook, S. A. and Reckhow, R. A., The relative efficiency of propositional proof systems, this Journal, vol. 44 (1979), no. 1, pp. 36–50.Google Scholar
[4]Krajíček, Jan, Exponentiation and second-order bounded arithmetic, Annals of Pure and Applied Logic, vol. 48 (1990), no. 3, pp. 261–276.CrossRefGoogle Scholar
[5]Krajíček, Jan, Bounded arithmetic, propositional logic, and complexity theory, Encyclopedia of Mathematics and its Applications, vol. 60, Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
[6]Krajíček, Jan, Diagonalization in proof complexity, Dec. 2003, preprint.Google Scholar
[7]Krajíček, Jan and Pudlák, Pavel, Propositional proof systems, the consistency of first order theories and the complexity of computations, this Journal, vol. 54 (1989), no. 3, pp. 1063–1079.Google Scholar
[8]Krajíček, Jan, Quantified propositional calculi and fragments of bounded arithmetic, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 36 (1990), pp. 29–46.CrossRefGoogle Scholar
[9]Krajíček, Jan and Takeuti, Gaisi, On bounded polynomial induction, Feasible mathematics (Buss, S. R. and Scott, P. J., editors), Birkhäuser Boston, 1990, pp. 259–280.CrossRefGoogle Scholar