Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-20T10:22:42.654Z Has data issue: false hasContentIssue false
  • English
  • Français

THE GAME OPERATOR ACTING ON WADGE CLASSES OF BOREL SETS

Published online by Cambridge University Press:  13 June 2019

GABRIEL DEBS  and
JEAN SAINT RAYMOND
GABRIEL DEBS
Affiliation:
SORBONNE UNIVERSITÉ UNIVERSITÉ PARIS DIDEROT, CNRS INSTITUT DE MATHÉMATIQUES DE JUSSIEU-PARIS RIVE GAUCHE IMJ-PRG, F-75005 PARIS, FRANCE and UNIVERSITÉ LE HAVRE NORMANDIE INSTITUT UNIVERSITAIRE DE TECHNOLOGIE RUE BORIS VIAN, BP 4006 76610 LE HAVRE, FRANCEE-mail: [email protected]
JEAN SAINT RAYMOND
Affiliation:
SORBONNE UNIVERSITÉ UNIVERSITÉ PARIS DIDEROT, CNRS INSTITUT DE MATHÉMATIQUES DE JUSSIEU-PARIS RIVE GAUCHE IMJ-PRG, F-75005 PARIS, FRANCE E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the behavior of the game operator 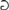$$ on Wadge classes of Borel sets. In particular we prove that the classical Moschovakis results still hold in this setting. We also characterize Wadge classes ${\bf{\Gamma }}$ for which the class 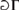has the substitution property. An effective variation of these results shows that for all 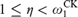$1 \le \eta < \omega _1^{{\rm{CK}}}$ and 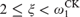$2 \le \xi < \omega _1^{{\rm{CK}}}$, 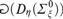is a Spector class while 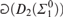is not.

Keywords

Primary 03E1528A05Secondary 54H05game operatorWadge classnormsscalessubstitution property
Type
Articles
Information
The Journal of Symbolic Logic , Volume 84 , Issue 3 , September 2019 , pp. 1224 - 1239
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Debs, G. and Saint Raymond, J., Borel liftings of Borel sets: Some decidable and undecidable statements.Memoirs of the American Mathematical Society, vol. 187 (2007), no. 876, MR2308388.Google Scholar
Debs, G. and Saint Raymond, J., On $$-complete sets. Proceedings of the American Mathematical Society, to appear.Google Scholar
Kechris, A., On the concept of $\Pi _1^1$-completenes. Proceedings of the American Mathematical Society, vol. 125 (1997), no. 6, pp. 1811–1814.Google Scholar
Kuratowski, K., Topology, vol. I, new edition, revised and augmented. Translated from the French by Jaworowski, J., Academic Press, New York-London; Państwowe Wydawnictwo Naukowe, Warsaw, 1997.Google Scholar
Louveau, A., Some results in the Wadge hierarchy of Borel sets, Wadge Degrees and Projective Ordinals: The Cabal Seminar, Volume II (Kechris, A. S., Löwe, B., and Steel, J. R., editors), Lecture Notes in Logic, vol. 37, Cambridge University Press, New York, 2012, pp. 47–73.Google Scholar
Louveau, A. and Saint Raymond, J., les propriétés de réduction et de norme pour les classes de Boréliens. Fundamenta Mathematicae, vol. 131 (1988), pp. 223–243.Google Scholar
Moschovakis, Y. N., Descriptive Set Theory, Studies in Logic, vol. 100, North-Holland, Amsterdam, 1979. Second edition, Mathematical Surveys and Monographs, vol. 155, American Mathematical Society, Providence, RI, 2009.Google Scholar