Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-27T15:59:27.007Z Has data issue: false hasContentIssue false
  • English
  • Français

Frege's unofficial arithmetic

Published online by Cambridge University Press:  12 March 2014

Agustín Rayo
Agustín Rayo*
Affiliation:
Department of Logic and Metaphysics, University of St Andrews, St Andrews, KY16 9AL, UK, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

I 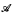show that any sentence of nth-order (pure or applied) arithmetic can be expressed with no loss of compositionality as a second-order sentence containing no arithmetical vocabulary, and use this result to prove a completeness theorem for applied arithmetic. More specifically. I set forth an enriched second-order language L. a sentence of L (which is true on the intended interpretation of L), and a compositionally recursive transformation Tr defined on formulas of L, and show that they have the following two properties: (a) in a universe with at least ℶn−2 objects, any formula of nth-order (pure or applied) arithmetic can be expressed as a formula of L, and (b) for any sentence 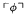of 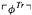is a second-order sentence containing no arithmetical vocabulary, and

Keywords

Second-order logicarithmeticlogicismnominalismFregeHodesBoolos
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 67 , Issue 4 , December 2002 , pp. 1623 - 1638
Copyright
Copyright © Association for Symbolic Logic 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Beaney, Michael (editor) [1997], The Frege reader, Blackwell, Oxford.Google Scholar
Benacerraf, Paul [1965], What numbers could not be, The Philosophical Review, vol. 74, pp. 47–73, Reprinted in Paul Benacerraf and Hilary Putnam, Philosophy of Mathematics.CrossRefGoogle Scholar
Benacerraf, Paul and Putnam, Hilary (editors) [1983], Philosophy of mathematics, second ed., Cambridge University Press, Cambridge.Google Scholar
Boolos, George [1984], To be is to be a value of a variable (or to be some values of some variables), The Journal of Philosophy, vol. 81, pp. 430–49, Reprinted in George Boolos, Logic, Logic and Logic.CrossRefGoogle Scholar
Boolos, George [1985a], Nominalist platonism, Philosophical Review, vol. 94, pp. 327–44, Reprinted in George Boolos, Logic, Logic and Logic.CrossRefGoogle Scholar
Boolos, George [1985b], Reading the Begriffsschrift, Mind, vol. 94, pp. 331–334, Reprinted in George Boolos, Logic, Logic and Logic.CrossRefGoogle Scholar
Boolos, George [1998], Logic, logic and logic, Harvard, Cambridge, Massachusetts.Google Scholar
Bostock, David [1979], Logic and arithmetic. Clarendon Press, Oxford.Google Scholar
Burgess, John and Rosen, Gideon [1997], A subject with no object, Oxford University Press, New York.Google Scholar
Frege, Gottlob [1884], Die Grundlagen der Arithmetik, English Translation by Austin, J.L., The Foundations of Arithmetic, Northwestern University Press, Evanston, IL, 1980.Google Scholar
Frege, Gottlob [1893/1903], Grundgesetze der Arithmetik, Vol 1 (1893), Vol 2 (1903). English Translation by Montgomery Furth, The Basic Laws of Arithmetic, University of California Press, Berkeley and Los Angeles, 1964.Google Scholar
Frege, Gottlob [1919], Notes for Ludwig Darmstaedter, Reprinted in Michael Beaney, The Frege Reader.Google Scholar
Hale, Bob [1997], Grundlagen 64, Proceedings of the Aristotelian Society, vol. 97, pp. 243–61, Reprinted in Bob Hale and Crispin Wright, The Reasons Proper Study.Google Scholar
Hale, Bob and Wright, Crispin [2001], The reason's proper study: Essays towards a neo-Fregean philosophy of mathematics, Clarendon Press.CrossRefGoogle Scholar
Heck, Richard (editor) [1997], Language, thought and logic, Clarendon Press, Oxford.CrossRefGoogle Scholar
Hodes, Harold T. [1984], Logicism and the ontological commitments of arithmetic, Journal of Philosophy, vol. 81, no. 3, pp. 123–149.CrossRefGoogle Scholar
Hodes, Harold T. [1990], Where do natural numbers come from?, Synthese, vol. 84, pp. 347–407.CrossRefGoogle Scholar
McGee, Vann [1997], How we learn mathematical language, Philosophical Review, vol. 106. no. 1, pp. 35–68.CrossRefGoogle Scholar
McGee, Vann [2000], Everything, In Gila Sher and Richard Tieszen. Between Logic and Intuition.Google Scholar
Rayo, Agustín [2002], Word and objects, Noûs, vol. 36, no. 3.CrossRefGoogle Scholar
Rayo, Agustín and Yablo, Stephen [2001], Nominalism through de-nominalization, Noûs, vol. 35, no. 1, pp. 74–92.CrossRefGoogle Scholar
Sher, Gila and Tieszen, Richard (editors) [2000], Between logic and intuition, Cambridge University Press, New York and Cambridge.CrossRefGoogle Scholar
Wright, Crispin [1983], Frege's conception of numbers as objects, Aberdeen University Press, Aberdeen.Google Scholar
Wright, Crispin [1997], The philosophical significance of Frege's theorem. In Richard Heck, Language Thought and Logic.Google Scholar