No CrossRef data available.
Article contents
A formalization of inductive logic
Published online by Cambridge University Press: 12 March 2014
Extract
In this note we show how Carnap's theory of degree of confirmation (inductive logic) may be constructed upon a very simple and restricted semantical basis. The semantical meta-languages here may either be based upon a relation of multiple denotation or may even be non-translational. To these meta-languages a suitable metric for sentences may be appended. Axioms for such meta-languages are suggested, so that an especially simple formalization of Carnap's inductive logic is in effect presented in outline.
For Carnap, inductive logic consists, roughly speaking, of a semantics augmented by a metric. More specifically, for a finite object-language 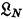 the semantics consists of a theory of designation for
the semantics consists of a theory of designation for 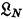 , and to this are added numerical functions on sentences of
, and to this are added numerical functions on sentences of 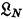 taking real numbers as values. (
taking real numbers as values. (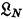 , it will be recalled, contains just N distinct individual constants as primitive, where ‘N’ is a constant standing for some fixed finite number.
, it will be recalled, contains just N distinct individual constants as primitive, where ‘N’ is a constant standing for some fixed finite number. 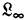 contains a denumerable infinity of distinct individual constants as primitive, and will be discussed in a moment.) Were we to formalize this theory we should have, then, a translation of
contains a denumerable infinity of distinct individual constants as primitive, and will be discussed in a moment.) Were we to formalize this theory we should have, then, a translation of 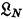 (or just
(or just 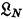 itself), a syntax for
itself), a syntax for 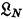 , a primitive relation of designation, real numbers, and several different kinds of class and relational variables. The character of the underlying syntax is not clear from Carnap's account, but this can easily be supplied by a suitable adaptation of Tarski's method. For this, variables for classes of and relations between the expressions of the object-language are needed. Also in Carnap's theory of designation, variables over relations between expressions and objects are needed fundamentally. Real numbers may be handled in various ways. To simplify, let us suppose these are introduced by having a special kind of variable to range over them. Then suitable axioms for real numbers may be given, e.g., one of the axiom sets of Tarski.
, a primitive relation of designation, real numbers, and several different kinds of class and relational variables. The character of the underlying syntax is not clear from Carnap's account, but this can easily be supplied by a suitable adaptation of Tarski's method. For this, variables for classes of and relations between the expressions of the object-language are needed. Also in Carnap's theory of designation, variables over relations between expressions and objects are needed fundamentally. Real numbers may be handled in various ways. To simplify, let us suppose these are introduced by having a special kind of variable to range over them. Then suitable axioms for real numbers may be given, e.g., one of the axiom sets of Tarski.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1958
References
1 Carnap, R., Logical foundations of probability ((University of Chicago Press, Chicago: 1950)Google Scholar.
2 See the author's On truth and multiple denotation, this Journal, vol. 18 (1953), pp. 1–8Google Scholar. Also his Truth and denotation, A study in semantical theory (Routledge and Kegan Paul, London; and University of Chicago Press, Chicago: 1958), pp. 99–142Google Scholar.
3 See the author's On non-translational semantics, Proceedings of the XIth International Congress of Philosophy (North-Holland Publishing Co., Amsterdam and Editions E. Nauwelaerts, Lou vain: 1953), Vol. V, pp. 132–138Google Scholar. Also Truth and denotation, pp. 179–212.
4 See, e.g., The concept of truth in formalized languages, in Logic, semantics, metamathematics, tr. by Woodger, J. H. (Clarendon Press, Oxford: 1956), pp. 152–278, especially pp. 167–185Google Scholar.
5 See Tarski, A., Introduction to logic (Oxford University Press, New York: 1941), pp. 213–218Google Scholar.
6 Quine, W. V., Mathematical logic, revised ed. (Harvard University Press, Cambridge: 1951), pp. 291–305Google Scholar. See also Truth and denotation, pp. 70–98.
7 See Tarski, op. cit., pp. 173–174.
8 See Truth and denotation, pp. 108–110.
9 See Martin, R. M., The notion of analytic truth (University of Pennsylvania Press, Philadelphia: to appear)CrossRefGoogle Scholar. Cf. also Carnap, R., Introduction to semantics (Harvard University Press, Cambridge: 1942), pp. 58 ff.Google Scholar
10 Logical foundations of probability, pp. 302 ff.
11 I.e., there is an individual constant i occurring in c which consists of ‘a’ concatenated with a string of accents j such tha t no individual constant occurring in c consists of ‘a’ concatenated with j concatenated with another accent, and d does consist of ‘a’ concatenated with j concatenated with another accent. Cf. the treatment of accents in Truth and denotation.
12 Gödel, K., Die Vollständigkeit der Axiome des Logischen Funktionenkalküls, Monatshefte für Mathematik und Physik 37 (1930): pp. 349–360CrossRefGoogle Scholar.
13 See Carnap, R., Introduction to semantics (Harvard University Press, Cambridge: 1942), pp. 167 ff.Google Scholar
14 See Carnap, R., Meaning Postulates, Philosophical studies, vol. 3 (1952): pp. 65–73CrossRefGoogle Scholar. Cf. also the review of Logical foundations of probability by J. Kemeny, this Journal, vol. 16 (1951), pp. 205–207.
15 Cf. The notion of analytic truth.
16 Cf. Truth and denotation, pp. 276–278.


