Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-16T23:11:36.514Z Has data issue: false hasContentIssue false
  • English
  • Français

Extending Baire property by uncountably many sets

Published online by Cambridge University Press:  12 March 2014

Paweł Kawa  and
Janusz Pawlikowski
Paweł Kawa
Affiliation:
Institute of Mathematics, Polish Academy of Sciences, Ul. Śniadeckich 8, 00-956 Warszawa, Poland. E-mail: [email protected]
Janusz Pawlikowski
Affiliation:
Institute of Mathematics, University of Wroclaw, Pl. Grunwaldzki 2/4 50-384 Wroclaw., Poland. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that for an uncountable κ in a suitable Cohen real model for any family {Av}v<κ of sets of reals there is a σ-homomorphism h from the σ-algebra generated by Borel sets and the sets Av, into the algebra of Baire subsets of 2κ modulo meager sets such that for all Borel B,

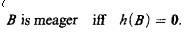
The proof is uniform, works also for random reals and the Lebesgue measure, and in this way generalizes previous results of Carlson and Solovay for the Lebesgue measure and of Kamburelis and Zakrzewski for the Baire property.

Keywords

Measure zeromeagerBorel setsBaire Propertyσ-algebra
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 75 , Issue 3 , September 2010 , pp. 896 - 904
Copyright
Copyright © Association for Symbolic Logic 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Banach, Stefan and Kazimierz, Kuratowski, Sur une généralization du problème de la measure, Fundamenta Mathematicae, vol. 14 (1929), pp. 127–131.CrossRefGoogle Scholar
[2]Baumgartner, J. E., Ineffability properties of cardinals, I, Infinite and finite sets, vol. I, North-Holland, Amsterdam, 1975, (Colloq., Keszthely, 1973; dedicated to P. Erdős on his 60th birthday), Colloq. Math. Soc. János Bolyai, vol. 10, pp. 109–130.Google Scholar
[3]Carlson, Tim, Extending Lebesgue measure by infinitely many sets. Pacific Journal of Mathematics, vol. 115 (1984), no. 1, pp. 33–45.CrossRefGoogle Scholar
[4]Fremlin, David H., Measure algebras, Handbook of Boolean algebras, vol. 3, North-Holland, Amsterdam, 1989, pp. 877–980.Google Scholar
[5]Kamburelis, Anastasis, A new proof of the Gitik-Shelah theorem, Israel Journal of Mathematics, vol. 72 (1990), no. 3, pp. 373–380.CrossRefGoogle Scholar
[6]Koppelberg, Sabine and Shelah, Saharon, Subalgebras of Cohen algebras need not be Cohen, Logic: from foundations to applications (Staffordshire, 1993), Oxford Science Publishing, Oxford University Press, New York, 1996, pp. 261–275.CrossRefGoogle Scholar
[7]Łoś, J. and Marczewski, E., Extensions of measure, Fundamenta Mathematicae, vol. 36 (1949), pp. 267–276.CrossRefGoogle Scholar
[8]Solovay, Robert M., Real-valued measurable cardinals, Axiomatic set theory, American Mathematical society, Providence, RI, 1971, (Proceedings of the Symposium on Pure Mathematics, vol. XIII, Part I, University of California, Los Angeles, California, 1967), pp. 397–428.CrossRefGoogle Scholar
[9]Zakrzewski, Piotr, Extending Baire property by countably many sets, Proceedings of the American Mathematical Society, vol. 129 (2001), no. 1, pp. 271–278.CrossRefGoogle Scholar