Article contents
Equality in 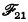
Published online by Cambridge University Press: 12 March 2014
Extract
In [CLg. II, §15B6], the problem of representing equality in the system 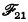 by means of an ob Q is discussed; it is shown there that if Q is taken to be a canonical atom of degree 2 and if the axiom scheme
by means of an ob Q is discussed; it is shown there that if Q is taken to be a canonical atom of degree 2 and if the axiom scheme
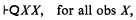
is postulated, then it follows by Rule Eq that

and, if no other properties are postulated for Q, then the converse of (1), Q-consistency, also holds. However, it is also desirable to have, in addition, the property

at least for some obs Z, and the statement is made in [CLg. II, §15B6] that no known way of incorporating this principle existed (at the time this statement was written) in such a way that there was a proof of Q-consistency. In this paper it is shown that if Z is restricted to be a basic canob of degree 1, i.e., if Z is restricted to be a predicate of one argument, then a system in which (2) is postulated can be proved Q-consistent.
The notations and conventions of [CLg. II] especially §15B, will be used throughout the paper.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1973
References
REFERENCE
- 1
- Cited by


