Article contents
The entire NS ideal on 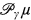 can be precipitous
can be precipitous
Published online by Cambridge University Press: 12 March 2014
Extract
The main result of this note is showing that if γ and μ are regular uncountable cardinals with γ ≤ μ then the non-stationary ideal (henceforth the NS ideal) on 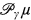 can be precipitous. This strengthens a result of [1] showing, under the same hypotheses, that a restriction of this ideal can be precipitous. See [1, Theorem 29, p. 36]. In fact, we show that even the strongly NS ideal on
can be precipitous. This strengthens a result of [1] showing, under the same hypotheses, that a restriction of this ideal can be precipitous. See [1, Theorem 29, p. 36]. In fact, we show that even the strongly NS ideal on 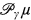 is precipitous in our model (since the former ideal is a restriction of the latter, the latter's being precipitous is a stronger assertion).
is precipitous in our model (since the former ideal is a restriction of the latter, the latter's being precipitous is a stronger assertion).
More precisely, by starting with a model of “ZFC + ‘κ is a supercompact cardinal’ + ‘μ < κ is a regular uncountable cardinal’ ”, we generate a model of ZFC where all cardinals below and including μ are not collapsed and where the NS and strongly NS ideals on Pγμ are precipitous, for all regular uncountable γ which are less than or equal to μ.
As far as consistency strength, we can obtain the same result even if κ is only Woodin in the ground model. However, the proof of this result is more complicated than in the case when κ is a supercompact cardinal. Furthermore, there are essentially no new ideas in adapting the proof relative to a supercompact cardinal to that relative to a Woodin cardinal beyond what appears in, e.g., [2]. We therefore give the complete proof relative to the existence of a supercompact cardinal and then briefly sketch the proof relative to the existence of a Woodin cardinal, using [2] as a reference.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1997
References
REFERENCES
- 7
- Cited by


