No CrossRef data available.
Article contents
Abstract
Building on Pierre Simon’s notion of distality, we introduce distality rank as a property of first-order theories and give examples for each rank m such that
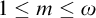 $1\leq m \leq \omega $
. For NIP theories, we show that distality rank is invariant under base change. We also define a generalization of type orthogonality called m-determinacy and show that theories of distality rank m require certain products to be m-determined. Furthermore, for NIP theories, this behavior characterizes m-distality. If we narrow the scope to stable theories, we observe that m-distality can be characterized by the maximum cycle size found in the forking “geometry,” so it coincides with
$1\leq m \leq \omega $
. For NIP theories, we show that distality rank is invariant under base change. We also define a generalization of type orthogonality called m-determinacy and show that theories of distality rank m require certain products to be m-determined. Furthermore, for NIP theories, this behavior characterizes m-distality. If we narrow the scope to stable theories, we observe that m-distality can be characterized by the maximum cycle size found in the forking “geometry,” so it coincides with
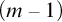 $(m-1)$
-triviality. On a broader scale, we see that m-distality is a strengthening of Saharon Shelah’s notion of m-dependence.
$(m-1)$
-triviality. On a broader scale, we see that m-distality is a strengthening of Saharon Shelah’s notion of m-dependence.
Keywords
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic



