Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-19T20:47:50.223Z Has data issue: false hasContentIssue false
  • English
  • Français

DERIVED MODELS OF MICE BELOW THE LEAST FIXPOINT OF THE SOLOVAY SEQUENCE

Published online by Cambridge University Press:  07 February 2019

DOMINIK ADOLF  and
GRIGOR SARGSYAN
DOMINIK ADOLF
Affiliation:
DEPARTMENT OF MATHEMATICS RUTGERS UNIVERSITY PISCATAWAY, NJ08854-8018, USAE-mail: [email protected]
GRIGOR SARGSYAN
Affiliation:
DEPARTMENT OF MATHEMATICS RUTGERS UNIVERSITY PISCATAWAY, NJ08854-8018, USAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce a mouse whose derived model satisfies 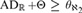$AD_ + {\rm{\Theta }} \ge \theta _{\aleph _2 } $. More generally, we will introduce a class of large cardinal properties yielding mice whose derived models can satisfy properties as strong as 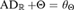$AD_ + {\rm{\Theta }} = \theta _{\rm{\Theta }} $.

Keywords

03E4503E60derived modelsmiceSolovay sequence
Type
Articles
Information
The Journal of Symbolic Logic , Volume 84 , Issue 1 , March 2019 , pp. 27 - 53
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Closson, E. W., The solovay sequence in derived models associated to mice, Ph.D. thesis, University of California at Berkeley, 2008.Google Scholar
Larson, P. B., The Stationary Tower - Notes on a Course by W. Hugh Woodin, first ed., University Lecture Series, vol. 32, American Mathematical Society, Providence, RI, 2004.Google Scholar
Mitchell, W. J. and Steel, J. R., Fine Structure and Iteration Trees, first ed., Lecture Notes in Logic, vol. 3, Springer, Berlin, 1994.10.1007/978-3-662-21903-4CrossRefGoogle Scholar
Sargsyan, G., Hod mice and the mouse set conjecture, Memoirs of the American Mathematical Society, vol. 236 (2015), no. 1111, pp. 1–185.10.1090/memo/1111CrossRefGoogle Scholar
Sargsyan, G. and Trang, N., The largest Suslin axiom, submitted.Google Scholar
Schlutzenberg, F. and Trang, N., Scales in hybrid mice over ${\Cal R}$. Preprint, available at http://math.cmu.edu/namtrang/scales_frame-2.pdf.Google Scholar
Steel, J., Derived models associated to mice, Computational Prospects of Infinity, Part I: Tutorials (Chong, C., Feng, Q., Slaman, T. A., Woodin, W. H., and Yang, Y., editors), World Scientific Publishing, Singapore, 2008, pp. 105–193.10.1142/9789812794055_0003CrossRefGoogle Scholar
Steel, J., Local K-c-constructions, this Journal, vol. 72 (2007), no. 3, pp. 721–737.Google Scholar
Steel, J., The derived model theorem, Logic Colloquium 2006 (Cooper, S. B., Geuvers, H., Pillay, A., and Väänänen, J., editors), Cambridge University Press, Cambridge, 2009, pp. 280–327.Google Scholar
Steel, J., An Outline of Inner Model Theory, Handbook of Set Theory (Foreman, M. and Kanamori, A., editors), Springer, Amsterdam, 2010, pp. 1595–1684.10.1007/978-1-4020-5764-9_20CrossRefGoogle Scholar
Steel, J. and Woodin, W. H., HOD as a core model, Ordinal Definability and Recursion Theory (Kechris, A. S., Löwe, B., and Steel, J. R., editors), Lecture Notes in Logic, Cambridge University Press, Cambridge, 2016, pp. 257–346.10.1017/CBO9781139519694.010CrossRefGoogle Scholar
Trang, N., Determinacy in $L\left( {,\mu } \right)$. Journal of Mathematical Logic, vol. 14 (2014), no. 1, p. 1450006.10.1142/S0219061314500068CrossRefGoogle Scholar
Zhu, Y., Realizing an AD+-model as the derived model of a premouse, Ph.D. thesis, National University of Singapore, 2012.Google Scholar