Article contents
A derivation of number theory from ancestral theory
Published online by Cambridge University Press: 12 March 2014
Extract
Martin has shown that the notions of ancestral and class-inclusion are sufficient to develop the theory of natural numbers in a system containing variables of only one type.
The purpose of the present paper is to show that an analogous construction is possible in a system containing, beyond the quantificational level, only the ancestral and the ordered pair.
The formulae of our system comprise quantificational schemata and anything which can be obtained therefrom by writing pairs (e.g. (x; y), ((x; y); (x; (y; y))) etc.) for free variables, or by writing ancestral abstracts (e.g. (*xyFxy) etc.) for schematic letters, or both.
The ancestral abstract (*xyFxy) means what is usually meant by 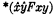 ; and the formula (*xyFxy)zw answers to Martin's (zw; xy)(Fxy).
; and the formula (*xyFxy)zw answers to Martin's (zw; xy)(Fxy).
The system presupposes a non-simple applied functional calculus of the first order, with a rule of substitution for predicate letters; over and above this it has three axioms for the ancestral and two for the ordered pair.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1952
References
1 See Martin, R. M., A homogeneous system for formal logic, this Journal, vol. 8 (1943), pp. 1–23Google Scholar (henceforth Martin1); also A note on nominalism and recursive functions, this Journal, vol. 14 (1949), pp. 27–32Google Scholar (henceforth Martin2); and On virtual classes and real numbers, this Journal, vol. 15 (1950), pp. 131–4Google Scholar.
2 Martin uses a generalized ancestral of any 2n-adic relation (Martin1, p. 4). For our purposes, the dyadic case suffices.
3 Strictly, the part-whole relation; but the reviewer of Martin1 (McKinsey) interprets it as class-inclusion; and the presence of the null-individual N makes this the more natural interpretation.
4 Martin1, pp. 15–23; Martin2, pp. 30–31.
5 The schematic letters F, G, etc. form an integral part of the system, and are not mere metalinguistic conventions as in Martin (see Martin1, p. 8.). This is necessary because there are no primitive predicates in our system.
6 R8 (4), Martin1, p. 12. I am grateful to Dr. Martin for having pointed this out to me.
7 The theory of ancestrals is taken in this paper to include Martin's R8 (1)–(4) (Martin1' pp. 11–12) and 2.27-2.2725 (Martin1, p. 15, Martin2, p. 29–30) and my AI1 and AI2. See footnote 11 below.
8 Cf. e.g. Hilbert, and Bernays, , Grundlagen der Mathematik, vol. 1, p. 164Google Scholar.
9 t is a parameter; i.e. it is free in 0 and in all the expressions (e.g. Nx, Fxyz, + xyz) defined in terms of 0. Strictly we should write 0t, Nix, ![]() , + txyz etc. to remind ourselves that t is free in these expressions. Analogous remarks apply to the H in D3; the case is different, however, in that we shall make no mistakes even if we forget that H occurs in all identity contexts. Cf. Quine, , Towards a calculus of concepts, this Journal, vol. 1 (1936), p. 7Google Scholar, remark on D3.
, + txyz etc. to remind ourselves that t is free in these expressions. Analogous remarks apply to the H in D3; the case is different, however, in that we shall make no mistakes even if we forget that H occurs in all identity contexts. Cf. Quine, , Towards a calculus of concepts, this Journal, vol. 1 (1936), p. 7Google Scholar, remark on D3.
10 This construction is due to Chwistek, L.. cf. The limits of science, p. 95Google Scholar.
11 Identity theory is taken in this paper to include quantification theory; similarly quantification theory is taken to include the propositional calculus, and ancestral theory to include quantification theory. None is taken to include couple theory.
12 Martin's 2.2721 (Martin2, p. 29).
13 Cf. Quine, , Mathematical logic, pp. 253–62Google Scholar.
14 Most of the theorems following correspond closely, both in content and in method of proof to theorems in Quine's Mathematical logic. DD9–10 correspond to DD44–45, POW1–3 to †682, †683 and †685; DD14–16 to DD46–8; and the six theorems of section 10 to ††690–695 respectively. It is unnecessary to add that the whole construction of sections 7 and 10 was suggested by Quine's work. Use of identity theory is largely tacit from here on.
15 Martin2, p. 30.
16 Martin's 2.2718 (Martin2, p. 29).
- 12
- Cited by


