Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T04:30:07.488Z Has data issue: false hasContentIssue false
  • English
  • Français

Degrees of unsolvability of continuous functions

Published online by Cambridge University Press:  12 March 2014

Joseph S. Miller
Joseph S. Miller*
Affiliation:
Department of Mathematics, Indiana University, Bloomington, IN 47405-5701, USA, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract.

We show that the Turing degrees are not sufficient to measure the complexity of continuous functions on [0, 1]. Computability of continuous real functions is a standard notion from computable analysis. However, no satisfactory theory of degrees of continuous functions exists. We introduce the continuous degrees and prove that they are a proper extension of the Turing degrees and a proper substructure of the enumeration degrees. Call continuous degrees which are not Turing degrees non-total. 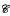Several fundamental results are proved: a continuous function with non-total degree has no least degree representation, settling a question asked by Pour-El and Lempp; every non-computable f ∈ [0,1] computes a non-computable subset of ℕ there is a non-total degree between Turing degrees a <Tb iff b is a PA degree relative to a; 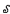⊆ 2ℕ is a Scott set iff it is the collection of f-computable subsets of ℕ for some f ∈ 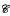[0,1] of non-total degree; and there are computably incomparable f, g ∈ 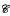[0,1] which compute exactly the same subsets of ℕ. Proofs draw from classical analysis and constructive analysis as well as from computability theory.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 69 , Issue 2 , June 2004 , pp. 555 - 584
Copyright
Copyright © Association for Symbolic Logic 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Arslanov, M. M., Nadyrov, R. F., and Solov'ev, V. D., A criterion for the completeness of recursively enumerable sets, and some generalizations of a fixed point theorem, Izestija Vysših Učebnyh Zavedeniǐ Matematika, (1977), no. 4 (179), pp. 3–7.Google Scholar
[2]Beeson, Michael J., Foundations of constructive mathematics, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], vol. 6, Springer-Verlag, Berlin, 1985.CrossRefGoogle Scholar
[3]Birkhoff, G. D. and Kellogg, O. D., Invariant points in function space, Transactions of the American Mathematical Society, vol. 23 (1922), no. 1, pp. 96–115.CrossRefGoogle Scholar
[4]Bohnenblust, H. F. and Karlin, S., On a theorem of Ville, Contributions to the theory of games, Annals of Mathematics Studies, no. 24, Princeton University Press, Princeton, N.J., 1950, pp. 155–160.Google Scholar
[5]Cenzer, D. and Remmel, J. B., classes in mathematics, Handbook of recursive mathematics, vol. 2, Studies in Logic and the Foundations of Mathematics, vol. 139, North-Holland, Amsterdam, 1998, pp. 623–821.Google Scholar
[6]Cenzer, Douglas, classes in computability theory, Handbook of computability theory, Studies in Logic and the Foundations of Mathematics, vol. 140, North-Holland, Amsterdam, 1999, pp. 37–85.CrossRefGoogle Scholar
[7]Cooper, S. B., Partial degrees and the density problem, this Journal, vol. 47 (1982), no. 4, pp. 854–859 (1983).Google Scholar
[8]Eilenberg, Samuel and Montgomery, Deane, Fixed point theorems for multi-valued transformations, American Journal of Mathematics, vol. 68 (1946), pp. 214–222.CrossRefGoogle Scholar
[9]Grzegorczyk, Andrzej, Computable functionals, Fundamenta Mathematicae, vol. 42 (1955), pp. 168–202.CrossRefGoogle Scholar
[10]Grzegorczyk, Andrzej, On the definitions of computable real continuous functions, Fundamenta Mathematicae, vol. 44 (1957), pp. 61–71.CrossRefGoogle Scholar
[11]Gutteridge, Lance, Some results on enumeration reducibility, Ph.D. thesis, Simon Fraser University, 1971.Google Scholar
[12]Jockusch, Carl G. Jr., and Soare, Robert I., classes and degrees of theories, Transactions of the American Mathematical Society, vol. 173 (1972), pp. 33–56.Google Scholar
[13]Kakutani, Shizuo, A generalization of Brouwer's fixed point theorem, Duke Mathematical Journal, vol. 8 (1941), pp. 457–459.CrossRefGoogle Scholar
[14]Kleene, Stephen Cole, Introduction to Metamathematics, D. Van Nostrand Company, Incorporation, New York, N.Y., 1952.Google Scholar
[15]Kreitz, Christoph and Weihrauch, Klaus, Theory of representations, Theoretical Computer Science, vol. 38 (1985), no. 1, pp. 35–53.CrossRefGoogle Scholar
[16]Lacombe, Daniel, Extension de la notion de fonction récursive aux fonctions d'une ou plusieurs variables réelles. I, Comptes Rendus Mathématique. Académie des Sciences. Paris, vol. 240 (1955). pp. 2478–2480.Google Scholar
[17]Lacombe, Daniel, Extension de la notion de fonction récursive aux fonctions d'une ou plusieurs variables réelles. II, III, Comptes Rendus Mathématique. Académie des Sciences. Paris, vol. 241 (1955), pp. 13–14, 151–153.Google Scholar
[18]Lacombe, Daniel, Quelques procédés de définition en topologie recursive, Constructivity in mathematics:Proceedings of the Colloquium held at Amsterdam, 1957 (Heyting, A., editor), Studies in Logic and the Foundations of Mathematics, North-Holland Publishing Company, 1959, pp. 129–158.Google Scholar
[19]Lerman, Manuel, Degrees of Unsolvability, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1983.CrossRefGoogle Scholar
[20]Medvedev, Yu. T., Degrees of difficulty of the mass problem, Doklady Akademii Nauk SSSR, vol. 104 (1955), pp. 501–504.Google Scholar
[21]Mučnik, A. A., On strongand weak reducibility of algorithmic problems, Akademija Nauk SSSR. Sibirskoe Otdelenie. Sibirskiĭ Matematičeskiĭ Žurnal, vol. 4 (1963), pp. 1328–1341.Google Scholar
[22]Myhill, John, Note on degrees of partial functions, Proceedings of the American Mathematical Society, vol. 12 (1961), pp. 519–521.CrossRefGoogle Scholar
[23]Nerode, Anil and Shore, Richard A., Second order logic and first order theories of reducibility orderings, The Kleene Symposium (Proceedings of the Symposium, University of Wisconsin, Madison, Wisconsin, 1978), Studies in Logic and the Foundations of Mathematics, vol. 101, North-Holland, Amsterdam, 1980, pp. 181–200.Google Scholar
[24]Orevkov, V. P., A constructive map of the square into itself, which moves every constructive point, Doklady Akademii Nauk SSSR, vol. 152 (1963), pp. 55–58.Google Scholar
[25]Posner, David B., The upper semilattice of degrees ≤ 0′ is complemented, this Journal, vol. 46 (1981), no. 4, pp. 705–713.Google Scholar
[26]Pour-El, Marian B. and Caldwell, Jerome, On a simple definition of computable function of a real variable—with applications to functions of a complex variable, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 21 (1975), pp. 1–19.CrossRefGoogle Scholar
[27]Pour-El, Marian B. and Richards, J. IAN, Computability and noncomputability in classical analysis, Transactions of the American Mathematical Society, vol. 275 (1983), no. 2, pp. 539–560.CrossRefGoogle Scholar
[28]Pour-El, Marian B. and Richards, J. IAN, Computability in Analysis and Physics, Springer-Verlag, Berlin, 1989.CrossRefGoogle Scholar
[29]Richter, Linda Jean, Degrees of structures, Ph.D. thesis, University of Illinois at Urbana-Champaign, 1979.Google Scholar
[30]Rogers, Hartley Jr., Theory of Recursive Functions and Effective Computability, McGraw-Hill Book Company, New York, 1967.Google Scholar
[31]Rozinas, M., The semilattice of e-degrees, Recursive functions (Russian), Ivanov. Gos. Univ., Ivanovo, 1978, pp. 71–84.Google Scholar
[32]Sacks, Gerald E., The recursively enumerable degrees are dense, Annals of Mathematics, Second Series, vol. 80 (1964), pp. 300–312.CrossRefGoogle Scholar
[33]Schauder, J., Der Fixpunktsatz in Funktionalräumen, Studia Mathematica, vol. 2 (1930), pp. 171–180.CrossRefGoogle Scholar
[34]Scott, Dana, Algebras of sets binumerable in complete extensions of arithmetic, Proceedings of Symposia in Pure Mathematics, Vol. V, American Mathematical Society, Providence, R.I., 1962, pp. 117–121.Google Scholar
[35]Selman, Alan L., Arithmetical reducibilities. I, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 17 (1971), pp. 335–350.CrossRefGoogle Scholar
[36]Simpson, Stephen G., Degrees of unsolvability: A survey of results, Handbook of Mathematical Logic (Barwise, J., editor), North-Holland, Amsterdam, 1977, pp. 631–652.CrossRefGoogle Scholar
[37]Simpson, Stephen G., First-order theory of the degrees of recursive unsolvability, Annals of Mathematics. Second Series, vol. 105 (1977), no. 1, pp. 121–139.CrossRefGoogle Scholar
[38]Slaman, Theodore A. and Woodin, W. Hugh, Definability in the enumeration degrees, Archive for Mathematical Logic, vol. 36 (1997). no. 4-5, pp. 255–267, Sacks Symposium (Cambridge, MA, 1993).CrossRefGoogle Scholar
[39]Spector, Clifford, On degrees of recursive unsolvability, Annals of Mathematics. Second Series, vol. 64 (1956), pp. 581–592.CrossRefGoogle Scholar
[40]Turing, A. M., On computable numbers, with an application to the Entscheidungsproblem, Proceedings of the London Mathematical Society. Second Series, vol. 42 (1936), pp. 230–265, Correction in [41].Google Scholar
[41]Turing, A. M., On computable numbers, with an application to the Entscheidungsproblem. A correction, Proceedings of the London Mathematical Society. Second Series, vol. 43 (1937), pp. 544–546, Correction to [40].Google Scholar
[42]Weihrauch, Klaus, Computability on computable metric spaces, Theoretical Computer Science, vol. 113 (1993), no. 2, pp. 191–210.CrossRefGoogle Scholar
[43]Weihrauch, Klaus, Computable Analysis, An Introduction, Springer-Verlag, Berlin, 2000.CrossRefGoogle Scholar