Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-19T20:43:38.775Z Has data issue: false hasContentIssue false
  • English
  • Français

DEFINABLE TOPOLOGICAL DYNAMICS

Published online by Cambridge University Press:  08 September 2017

KRZYSZTOF KRUPIŃSKI
KRZYSZTOF KRUPIŃSKI*
Affiliation:
INSTYTUT MATEMATYCZNYUNIWERSYTET WROCŁAWSKIPL. GRUNWALDZKI 2/4 50-384 WROCŁAW, POLANDE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a group G definable in a first order structure M we develop basic topological dynamics in the category of definable G-flows. In particular, we give a description of the universal definable G-ambit and of the semigroup operation on it. We find a natural epimorphism from the Ellis group of this flow to the definable Bohr compactification of G, that is to the quotient 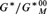${G^{\rm{*}}}/G_M^{{\rm{*}}00}$ (where G* is the interpretation of G in a monster model). More generally, we obtain these results locally, i.e., in the category of Δ-definable G-flows for any fixed set Δ of formulas of an appropriate form. In particular, we define local connected components 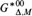$G_{{\rm{\Delta }},M}^{{\rm{*}}00}$ and 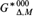$G_{{\rm{\Delta }},M}^{{\rm{*}}000}$, and show that 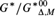${G^{\rm{*}}}/G_{{\rm{\Delta }},M}^{{\rm{*}}00}$ is the Δ-definable Bohr compactification of G. We also note that some deeper arguments from [14] can be adapted to our context, showing for example that our epimorphism from the Ellis group to the Δ-definable Bohr compactification factors naturally yielding a continuous epimorphism from the Δ-definable generalized Bohr compactification to the Δ-definable Bohr compactification of G. Finally, we propose to view certain topological-dynamic and model-theoretic invariants as Polish structures which leads to some observations and questions.

Keywords

03C4554H20model theorytopological dynamicsdefinable flows
Type
Articles
Information
The Journal of Symbolic Logic , Volume 82 , Issue 3 , September 2017 , pp. 1080 - 1105
Copyright
Copyright © The Association for Symbolic Logic 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Auslander, J., Minimal Flows and their Extensions, Mathematics Studies, vol. 153, North-Holland, The Netherlands, 1988.Google Scholar
Chernikov, A. and Simon, P., Definably amenable NIP groups, submitted.Google Scholar
Conversano, A. and Pillay, A., Connected components of definable groups and o-minimality I. Advances in Mathematics, vol. 231 (2012), pp. 605–623.Google Scholar
Ellis, R., Lectures on Topological Dynamics, Benjamin, W. A., New York, 1969.Google Scholar
Engelking, R., General Topology, Sigma Series in Pure Mathematics, Heldermann Verlag, Berlin, 1989.Google Scholar
Gismatullin, J., Model theoretic connected components of groups . Israel Journal of Mathematics, vol. 184 (2011), pp. 251–274.CrossRefGoogle Scholar
Gismatullin, J. and Krupiński, K., On model-theoretic connected components in some group extensions . Journal of Mathematical Logic, vol. 15 (2015), 1550009 (51 pages).CrossRefGoogle Scholar
Gismatullin, J., Penazzi, D., and Pillay, A., On compactifications and the topological dynamics of definable groups . Annals of Pure and Applied Logic, vol. 165 (2014), pp. 552–562.Google Scholar
Glasner, S., Proximal Flows, Lecture Notes in Mathematics, vol. 517, Springer, Germany, 1976.Google Scholar
Jagiella, G., Definable topological dynamics and real Lie groups . Mathematical Logic Quarterly, vol. 61 (2015), pp. 45–55.Google Scholar
Krupiński, K., Generalizations of small profinite structures , this JOURNAL, vol. 75 (2010), pp. 1147–1175.Google Scholar
Krupiński, K., Some model theory of Polish structures . Transactions of the American Mathematical Society, vol. 362 (2010), pp. 3499–3533.CrossRefGoogle Scholar
Krupiński, K. and Newelski, L., On bounded type definable equivalence relations . Notre Dame Journal of Formal Logic, vol. 43 (2002), pp. 231–242.Google Scholar
Krupiński, K. and Pillay, A., Generalized Bohr compactification and model-theoretic connected components . Mathematical Proceedings of the Cambridge Philosophical Society, to appear. Published on-line, doi: https://doi.org/10.1017/S0305004116000967.Google Scholar
Krupiński, K., Pillay, A., and Rzepecki, T., Topological dynamics and the complexity of strong types, submitted.Google Scholar
Krupiński, K. and Wagner, F., Small, nm-stable compact G-groups. Israel Journal of Mathematics, vol. 194 (2013), pp. 907–933.Google Scholar
Lascar, D. and Pillay, A., Hyperimaginaries and automorphism groups, this JOURNAL, vol. 66 (2001), pp. 127–143.Google Scholar
Newelski, L., ${\cal M}$ -gap conjecture and m-normal theories. Israel Journal of Mathematics, vol. 106 (1998), pp. 285–311.Google Scholar
Newelski, L., Small profinite structures . Transactions of the American Mathematical Society, vol. 354 (2001), pp. 925–943.Google Scholar
Newelski, L., Topological dynamics of definable groups actions, this JOURNAL, vol. 74 (2009), pp. 50–72.Google Scholar
Newelski, L., Model theoretic aspects of the Ellis semigroup . Israel Journal of Mathematics, vol. 190 (2012), pp. 477–507.Google Scholar
Pillay, A., Geometric Stability Theory, Clarendon Press, Oxford, 1996.Google Scholar
Pillay, A., Type-definability, compact Lie groups, and o-minimality . Journal of Mathematical Logic, vol. 4 (2004), pp. 147–162.Google Scholar
Ribes, L. and Zalesskii, P., Profinite Groups, vol. 40, Springer, Heidelberg, 2000.Google Scholar
Shelah, S., Minimal bounded index subgroup for dependent theories . Proceedings of the American Mathematical Society, vol. 136 (2008), pp. 1087–1091.Google Scholar
Shelah, S., Dependent dreams: Recounting types, preprint Sh:950.Google Scholar
Simon, P., A Guide to NIP Theories, Lecture Notes in Logic, Cambridge University Press, Cambridge, 2015.Google Scholar
Wagner, F., Small m-stable profinite groups . Fundamenta Mathematicae, vol. 176 (2003), pp. 181–191.Google Scholar
Yao, N. and Long, D., Topological dynamics for groups definable in real closed field. Annals of Pure and Applied Logic, vol. 166 (2015), pp. 261–273.Google Scholar