Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-30T20:30:53.942Z Has data issue: false hasContentIssue false
  • English
  • Français

Co-stationarity of the ground model

Published online by Cambridge University Press:  12 March 2014

Natasha Dobrinen  and
Sy-David Friedman
Natasha Dobrinen
Affiliation:
Kurt Gödel Research Center For Mathematical Logic, Universität Wien, Währingerstrasse 25, 1090 Wien, Austria.E-mail:[email protected], URL: http://www.logic.univie.ac.at/~dobrinen/
Sy-David Friedman
Affiliation:
Kurt Gödel Research Center For Mathematical Logic, Universität Wien, Währingerstrasse 25, 1090 Wien, Austria.E-mail:[email protected], URL: http://www.logic.univie.ac.at/~sdf/
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper investigates when it is possible for a partial ordering ℙ to force Pk(Λ)\V to be stationary in Vℙ. It follows from a result of Gitik that whenever ℙ adds a new real, then Pk(Λ)\V is stationary in Vℙ for each regular uncountable cardinal κ in Vℙ and all cardinals λ ≥ κ in Vℙ [4], However, a covering theorem of Magidor implies that when no new ω-sequences are added, large cardinals become necessary [7]. The following is equiconsistent with a proper class of ω1-Erdős cardinals: If ℙ is ℵ1-Cohen forcing, then Pk(Λ)\V is stationary in Vℙ, for all regular κ ≥ ℵ2and all λ ≩ κ. The following is equiconsistent with an ω1-Erdős cardinal: If ℙ is ℵ1-Cohen forcing, then 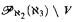is stationary in Vℙ. The following is equiconsistent with κ measurable cardinals: If ℙ is κ-Cohen forcing, then 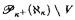is stationary in Vℙ.

Keywords

PkΛco-stationarityErdos cardinalmeasurable cardinal
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 71 , Issue 3 , September 2006 , pp. 1029 - 1043
Copyright
Copyright © Association for Symbolic Logic 2006

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Baumgartner, James E., On the size of closed unbounded sets, Annals of Pure and Applied Logic, vol. 54 (1991), pp. 195–227.CrossRefGoogle Scholar
[2]Beller, A., Jensen, R., and Welch, P., Coding the universe, Cambridge University Press, 1982.CrossRefGoogle Scholar
[3]Bukovsky, Lev and Coplakova, Eva, Minimal collapsing extensions of models of ZFC, Annals of Pure and Applied Logic, vol. 46 (1990), pp. 265–298.CrossRefGoogle Scholar
[4]Gitik, Moti, Nonsplitting subsets of , this Journal, vol. 50 (1985), no. 4, pp. 881–894.Google Scholar
[5]Koepke, Peter, Some applications of short cone models, Annals of Pure and Applied Logic, vol. 37 (1988), pp. 179–204.CrossRefGoogle Scholar
[6]Koppelberg, Sabine, Hanbook of Boolean algebra, vol. 1, North-Holland, 1989.Google Scholar
[7]Magidor, Menachem, Representing sets of ordinals as countable unions of sets in the core model, Transactions of American Mathematical Society, vol. 317 (1990), no. 1, pp. 91–126.CrossRefGoogle Scholar
[8]Menas, Telis K., On strong compactness and supercompactness, Annals of Mathematical Logic, vol. 7 (1974/1975), pp. 387–359.CrossRefGoogle Scholar
[9]Mitchell, William, The covering lemma, Handbook of set theory (Foreman, M., Kanamori, A., and Magidor, M., editors), Kluwer Academic Publishers, Dordrecht, to appear.Google Scholar
[10]Namba, Kanji, Independence proof of (ω1, ωα)-distributive law in complete Boolean algebras, Commentarii Mathematici Universitatis Sancti Pauli, vol. 19 (1971), pp. 1–12.Google Scholar
[11]Shelah, Saharon, Independence of strong partition relation for small cardinals, and the free-subset problem, this Journal, vol. 45 (1980), no. 3, pp. 505–509.Google Scholar
[12]Shelah, Saharon, Proper and improper forcing, second ed., Springer-Verlag, 1998.CrossRefGoogle Scholar