Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-09T23:59:48.709Z Has data issue: false hasContentIssue false
  • English
  • Français

A correction to Lewis and Langford's Symbolic logic

Published online by Cambridge University Press:  12 March 2014

J. C. C. McKinsey
J. C. C. McKinsey*
Affiliation:
New York University
Get access Rights & Permissions [Opens in a new window]

Extract

The purpose of this note is to call attention to a minor error in Lewis and Langford's Symbolic logic. On page 221, in discussing the Tarski-Łukasiewicz three-valued logic, the authors make the following assertion: “Let T(p) be any proposition, involving only one element, whose analogue holds in the two-valued system; if T(p) does not hold in the Three-valued Calculus, then pC.T(p) and Np.C.T(p) both hold.”

I shall show, by means of a counter-example, that this assertion is not true. Let T(p) be the sentence:

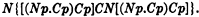
It is then easily verified that T(0) = T(1) = 1, and that T(½) = 0. Thus T(p) holds in the two-valued calculus, but not in the three-valued calculus. On the other hand, pC.T(p) does not hold, since ½.CT(½) = ½C0 = ½; similarly, Np.C.T(p) does not hold, since N½.C.T(½) = ½C0 = ½.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 5 , Issue 4 , December 1940 , pp. 149
Copyright
Copyright © Association for Symbolic Logic 1940

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1 Lewis, C. I. and Langford, C. H., Symbolic logic, New York and London 1932Google Scholar.