Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-24T16:45:56.025Z Has data issue: false hasContentIssue false
  • English
  • Français

COMPARING TWO VERSIONS OF THE REALS

Published online by Cambridge University Press:  12 August 2016

G. IGUSA  and
J. F. KNIGHT
G. IGUSA
Affiliation:
UNIVERSITY OF NOTRE DAME NOTRE DAME, IN 46556, USAE-mail: [email protected]
J. F. KNIGHT
Affiliation:
UNIVERSITY OF NOTRE DAME NOTRE DAME, IN 46556, USAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Schweber [10] defined a reducibility that allows us to compare the computing power of structures of arbitrary cardinality. Here we focus on the ordered field 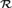${\cal R}$ of real numbers and a structure 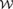${\cal W}$ that just codes the subsets of ω. In [10], it was observed that 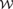${\cal W}$ is reducible to 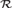${\cal R}$. We prove that 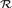${\cal R}$ is not reducible to 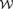${\cal W}$. As part of the proof, we show that for a countable recursively saturated real closed field 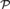${\cal P}$ with residue field k, some copy of 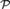${\cal P}$ does not compute a copy of k.

Keywords

computabilityuncountable structures
Type
Articles
Information
The Journal of Symbolic Logic , Volume 81 , Issue 3 , September 2016 , pp. 1115 - 1123
Copyright
Copyright © The Association for Symbolic Logic 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ash, C. J. and Knight, J. F., Computable Structures and the Hyperarithmetical Hierarchy, Elsevier, Amsterdam, 2000.Google Scholar
Ash, C. J., Knight, J. F., Manasse, M., and Slaman, T., Generic copies of countable structures . Annals of Pure and Applied Logic, vol. 42 (1989), pp. 195–205.Google Scholar
Barwise, J. and Schlipf, J., An introduction to recursively saturated and resplendent models, this Journal, vol. 41 (1976), pp. 531–536.Google Scholar
Chisholm, J., Effective model theory vs. recursive model theory, this Journal, vol. 55 (1990), pp. 1168–1191.Google Scholar
Downey, R., Greenberg, N., and Miller, J., Generic Muchnik reducibility and presentations of fields . Israel Journal of Mathematics, to appear.Google Scholar
Friedberg, R., Three theorems on recursive enumerations, this Journal, vol. 23 (1958), pp. 309–316.Google Scholar
Igusa, G., Knight, J. F., and Schweber, N., Computing strength of structures related to the field of real numbers, preprint.Google Scholar
Knight, J. F., Degrees coded in jumps of orderings, this Journal, vol. 51 (1986), pp. 1034–1042.Google Scholar
Knight, J. F. and Lange, K., Complexity of structures associated with real closed fields . Proceedings of the London Mathematical Society, vol. 107 (2013), pp. 177–197.Google Scholar
Knight, J. F., Montalbán, A., and Schweber, N., Computable structures in generic extensions, this Journal, to appear.Google Scholar
Kunen, K., Set Theory: An Introduction to Independence Proofs, Studies in Logic and the Foundations of Mathematics, Elsevier, Amsterdam, 1980.Google Scholar
Macintyre, A. and Marker, D., Degrees of recursively saturated models . Transactions of the American Mathematical Society, vol. 282 (1984), pp. 539–554.Google Scholar
van den Dries, L., Algebraic theories with definable Skolem functions, this Journal, vol. 49 (1984), pp. 625–629.Google Scholar