Hostname: page-component-6dbcb7884d-4tctr Total loading time: 0 Render date: 2025-02-14T08:24:13.576Z Has data issue: false hasContentIssue false
  • English
  • Français

CICHOŃ’S MAXIMUM WITH EVASION NUMBER

Published online by Cambridge University Press:  27 January 2025

TAKASHI YAMAZOE
TAKASHI YAMAZOE*
Affiliation:
GRADUATE SCHOOL OF SYSTEM INFORMATICS KOBE UNIVERSITY, ROKKO–DAI 1–1 NADA–KU, 657–8501 KOBE JAPAN
*
E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that the evasion number 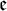$\mathfrak {e}$ can be added to Cichoń’s maximum with a distinct value. More specifically, it is consistent that 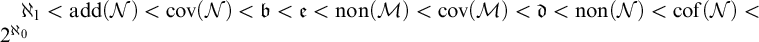$\aleph _1<\operatorname {\mathrm {add}}(\mathcal {N})<\operatorname {\mathrm {cov}}(\mathcal {N})<\mathfrak {b}<\mathfrak {e}<\operatorname {\mathrm {non}}(\mathcal {M})<\operatorname {\mathrm {cov}}(\mathcal {M})<\mathfrak {d}<\operatorname {\mathrm {non}}(\mathcal {N})<\operatorname {\mathrm {cof}}(\mathcal {N})<2^{\aleph _0}$ holds.

Keywords

cardinal invariantsCichoń’s maximumevasion numberultrafilter-limit
Type
Article
Information
The Journal of Symbolic Logic , First View , pp. 1 - 31
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bartoszynski, T., Invariants of measure and category , Handbook of Set Theory . Vols. 1, 2, 3, Springer, Dordrecht, 2010, pp. 491–555.Google Scholar
Bartoszynski, T. and Shelah, S., Closed measure zero sets . Annals of Pure and Applied Logic , vol. 58 (1992), no. 2, pp. 93–110.CrossRefGoogle Scholar
Brendle, J., Cardona, M. A., and Mejía, D. A., Filter-linkedness and its effect on preservation of cardinal characteristics . Annals of Pure and Applied Logic , vol. 172 (2021), no. 1, Paper 102856, 30.CrossRefGoogle Scholar
Brendle, J., Cardona, M. A., and Mejía, D. A., Separating cardinal characteristics of the strong measure zero ideal, preprint, 2023, arXiv:2309.01931.Google Scholar
Bartoszyński, T. and Judah, H., Set theory . On the Structure of the Real Line , A K Peters, Ltd., Wellesley, 1995.Google Scholar
Blass, A., Cardinal characteristics and the product of countably many infinite cyclic groups . Journal of Algebra , vol. 169 (1994), no. 2, pp. 512–540.CrossRefGoogle Scholar
Brendle, J., Larger cardinals in Cichoń’s diagram . The Journal of Symbolic Logic , vol. 56 (1991), no. 3, pp. 795–810.Google Scholar
Brendle, J. , Evasion and prediction-the Specker phenomenon and Gross spaces . Forum Mathematicum , vol. 7(1995), Jahresband, pp. 513–542 CrossRefGoogle Scholar
Brendle, J. and Shelah, S., Evasion and prediction II . Journal of the London Mathematical Society , vol. 53 (1996), no. 1, pp. 19–27.CrossRefGoogle Scholar
Cardona, M. A. and Mejía, D. A., Forcing constellations of Cichoń’s diagram by using the Tukey order, Ky $\bar{\mathrm{o}}$ to Daigaku S $\bar{\mathrm{u}}$ rikaiseki Kenky $\bar{\mathrm{u}}$ sho K $\bar{\mathrm{o}}$ ky $\bar{\mathrm{u}}$ roku, 2213 (2022), 14–17.Google Scholar
Cardona, M. A., Mejía, D. A., and Uribe-Zapata, A. F., Controlling the uniformity of the ideal generated by the ${F}_{\sigma }$ measure zero subsets of the reals. RIMS Set Theory Workshop 2023, https://tenasaku.com/RIMS2023/slides/cardona-rims2023.pdf, 2023.Google Scholar
Cardona, M. A., Mejía, D. A., and Uribe-Zapata, A. F., Two-dimensional iterations with fam-limits , RIMS Set Theory Workshop, 2023, https://tenasaku.com/RIMS2023/slides/mejia-20231027RIMS.pdf, 2023.Google Scholar
Engelking, R. and Karłowicz, M., Some theorems of set theory and their topological consequences . Fundamenta Mathematicae , vol. 57 (1965), no. 3, pp. 275–285.CrossRefGoogle Scholar
Fuchino, S. and Mejía, D. A., Variations of the negation of Riis’ axiom , First Brazil–Colombia Meeting in Logic, 2021.Google Scholar
Goldstern, M., Kellner, J., Mejía, D. A., and Shelah, S., Controlling cardinal characteristics without adding reals. Journal of Mathematical Logic, vol. 21 (2021), no. 03, pp. 2150018.CrossRefGoogle Scholar
Goldstern, M., Kellner, J., Mejía, D. A., and Shelah, S., Preservation of splitting families and cardinal characteristics of the continuum . Israel Journal of Mathematics , vol. 246 (2021), no. 1, pp. 73–129.CrossRefGoogle Scholar
Goldstern, M., Kellner, J., Mejía, D. A., and Shelah, S., Adding the evasion number to Cichoń’s Maximum , XVI International Luminy Workshop in Set Theory, 2021, https://dmg.tuwien.ac.at/kellner/2021˙Luminy˙talk.pdf.Google Scholar
Goldstern, M., Kellner, J., Mejía, D. A., and Shelah, S., Cichoń’s maximum without large cardinals . Journal of the European Mathematical Society , vol. 24 (2022), no. 11, pp. 3951–3967.CrossRefGoogle Scholar
Goldstern, M., Kellner, J., and Shelah, S., Cichoń’s maximum . Annals of Mathematics (2) , vol. 190 (2019), no. 1, pp. 113–143.CrossRefGoogle Scholar
Goldstern, M., Mejía, D. A., and Shelah, S., The left side of Cichoń’s diagram . Proceedings of the American Mathematical Society , vol. 144 (2016), no. 9, pp. 4025–4042.CrossRefGoogle Scholar
Judah, H. and Shelah, S., The Kunen-Miller chart (Lebesgue measure, the Baire property, Laver reals and preservation theorems for forcing) . The Journal of Symbolic Logic , vol. 55 (1990), no. 3, pp. 909–927.CrossRefGoogle Scholar
Kamburelis, A., Iterations of Boolean algebras with measure . Archive for Mathematical Logic , vol. 29 (1989), pp. 21–28.CrossRefGoogle Scholar
Kellner, J., Shelah, S., and Tănasie, A. R., Another ordering of the ten cardinal characteristics in Cichoń’s diagram . Commentationes Mathematicae Universitatis Carolinae , vol. 60 (2019), no. 1, pp. 61–95.Google Scholar
Mejía, D. A., Matrix iterations and Cichoń’s diagram . Archive for Mathematical Logic , vol. 52 (2013), no. 3–4, pp. 261–278.Google Scholar
Mejía, D. A., Matrix iterations with vertical support restrictions , Proceedings of the 14th and 15th Asian Logic Conferences , World Scientific Publishing, Hackensack, NJ, 2019, pp. 213–248.CrossRefGoogle Scholar
Shelah, S., Covering of the null ideal may have countable cofinality . Fundamenta Mathematicae , vol. 166 (2000), no. 1–2, pp. 109–136.CrossRefGoogle Scholar
Uribe-Zapata, A. F., Iterated forcing with finitely additive measures: applications of probability to forcing theory , Master’s thesis, Universidad Nacional de Colombia, sede Medellín, 2023.Google Scholar