Article contents
Cardinal functions on ultra products of Boolean algebras
Published online by Cambridge University Press: 12 March 2014
Extract
This article is concerned with functions k assigning a cardinal number to each infinite Boolean algebra (BA), and the behaviour of such functions under ultraproducts. For some common functions k we have
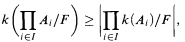
for others we have ≤ instead, under suitable assumptions. For the function π character we go into more detail. More specifically, ≥ holds when F is regular, for cellularity, length, irredundance, spread, and incomparability. ≤ holds for π. ≥ holds under GCH for F regular, for depth, π, πχ, χ, h-cof, tightness, hL, and hd. These results show that ≥ can consistently hold in ZFC since if V = L holds then all uniform ultrafilters are regular. For π-character we prove two more results: (1) If F is regular and ess 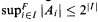 , then
, then
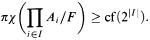
(2) It is relatively consistent to have 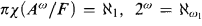 , where A is the denumerable atomless BA.
, where A is the denumerable atomless BA.
A thorough analysis of what happens without the assumption that F is regular can be found in Rosłanowski, Shelah [8] and Magidor, Shelah [5]. Those papers also mention open problems concerning the above two possible inequalities.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1997
References
REFERENCES
- 1
- Cited by


