Article contents
Canonical bases in excellent classes
Published online by Cambridge University Press: 12 March 2014
Abstract
We show that any (atomic) excellent class 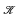 can be expanded with hyperimaginaries to form an (atomic) excellent class
can be expanded with hyperimaginaries to form an (atomic) excellent class 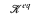 which has canonical bases. When
which has canonical bases. When 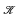 is, in addition, of finite U-rank, then
is, in addition, of finite U-rank, then 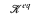 is also simple and has a full canonical bases theorem. This positive situation contrasts starkly with homogeneous model theory for example, where the eq-expansion may fail to be homogeneous. However, this paper shows that expanding an ω-stable, homogeneous class
is also simple and has a full canonical bases theorem. This positive situation contrasts starkly with homogeneous model theory for example, where the eq-expansion may fail to be homogeneous. However, this paper shows that expanding an ω-stable, homogeneous class 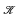 gives rise to an excellent class, which is simple if
gives rise to an excellent class, which is simple if 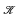 is of finite U-rank.
is of finite U-rank.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2008
References
REFERENCES
- 1
- Cited by


