Article contents
Bounding homogenous models
Published online by Cambridge University Press: 12 March 2014
Abstract
A Turing degree d is homogeneous bounding if every complete decidable (CD) theory has a d-decidable homogeneous model 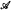 , i.e., the elementary diagram De (
, i.e., the elementary diagram De (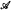 ) has degree d. It follows from results of Macintyre and Marker that every PA degree (i.e., every degree of a complete extension of Peano Arithmetic) is homogeneous bounding. We prove that in fact a degree is homogeneous bounding if and only if it is a PA degree. We do this by showing that there is a single CD theory T such that every homogeneous model of T has a PA degree.
) has degree d. It follows from results of Macintyre and Marker that every PA degree (i.e., every degree of a complete extension of Peano Arithmetic) is homogeneous bounding. We prove that in fact a degree is homogeneous bounding if and only if it is a PA degree. We do this by showing that there is a single CD theory T such that every homogeneous model of T has a PA degree.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2007
References
REFERENCES
- 2
- Cited by


