Article contents
Axioms for strong reduction in combinatory logic
Published online by Cambridge University Press: 12 March 2014
Extract
In combinatory logic there is a system of objects which intuitively represent functions, and a binary relation between these objects, which represents the process of evaluating the result of applying a function to an argument. (This is explained fully in [1].) From this relation called weak reduction, “≥,” an equivalence relation is defined by saying that X is weakly equivalent to Y if and only if there exist n (with 0 ≤ n) and X0,…,Xη such that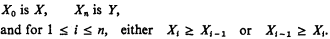
It turns out that equivalent objects represent the same function, but two objects representing the same function need not be equivalent.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1967
References
- 8
- Cited by


