Published online by Cambridge University Press: 27 October 2020
Let 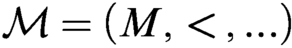 $\mathcal M=(M,<,\ldots)$ be a linearly ordered first-order structure and T its complete theory. We investigate conditions for T that could guarantee that
$\mathcal M=(M,<,\ldots)$ be a linearly ordered first-order structure and T its complete theory. We investigate conditions for T that could guarantee that  $\mathcal M$ is not much more complex than some colored orders (linear orders with added unary predicates). Motivated by Rubin’s work [5], we label three conditions expressing properties of types of T and/or automorphisms of models of T. We prove several results which indicate the “geometric” simplicity of definable sets in models of theories satisfying these conditions. For example, we prove that the strongest condition characterizes, up to definitional equivalence (inter-definability), theories of colored orders expanded by equivalence relations with convex classes.
$\mathcal M$ is not much more complex than some colored orders (linear orders with added unary predicates). Motivated by Rubin’s work [5], we label three conditions expressing properties of types of T and/or automorphisms of models of T. We prove several results which indicate the “geometric” simplicity of definable sets in models of theories satisfying these conditions. For example, we prove that the strongest condition characterizes, up to definitional equivalence (inter-definability), theories of colored orders expanded by equivalence relations with convex classes.