Analytic inductive definitions

Extract

An operator Γ mapping P(ω) to itself is inductive if Γ(A) ⊇ A for all A. For such an inductive operator Γ we define {Γ^α : α ∈ ORD} by letting Γ = ⌀, Γ^{α + 1} = Γ(Γ^α ) for all α, and Γ^β = ⋃{Γ^α : α < β} for limit ordinals β. The closure ordinal ∣Γ∣ of Γ is the least ordinal α such that Γ^α+1 = Γ^α and the closure 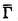is Γ^∣Γ∣.

Let 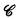be a class of operators over the natural numbers. The closure ordinal ∣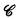∣ of 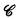is the supremum of {∣Γ∣: Γ is an inductive operator and 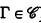}. The closure algebra 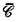generated by 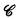is {A ⊆ ω: A is 1-1 reducible to 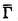for some inductive operator 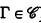}. The inductive algebra 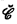generated by 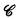is {Γ^α : Γ is an inductive operator in 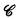and α < ∣Γ∣}.

For A ∈ P(ω), 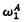is the supremum of the ordinals of well-orderings recursive in A. For 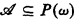, let 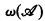be the supremum of 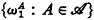. For example, it is well known that ω(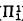) = ω(∆₁ ⁰ = ω ₁, ω(Π₁ ¹) = ω ₁ and ω(Δ_n ¹) = δ_n ¹ for n > 1 (the latter by definition).