No CrossRef data available.
Article contents
An algebraic characterization of power set in countable standard models of ZF1
Published online by Cambridge University Press: 12 March 2014
Extract
The following is a classical result:
Theorem 1.1. A complete atomic Boolean algebra is isomorphic to a power set algebra [2, p. 70].
One of the consequences of [3] is: If M is a countable standard model of ZF and 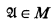 is a countable (in M) model of a complete ℵ0-categorical theory T, then there is a countable standard model N of ZF and a Λ ∈ N such that the Boolean algebra of definable (in T with parameters from
is a countable (in M) model of a complete ℵ0-categorical theory T, then there is a countable standard model N of ZF and a Λ ∈ N such that the Boolean algebra of definable (in T with parameters from 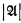 ) subsets of
) subsets of 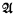 is isomorphic to the power set algebra of Λ in N. In particular if
is isomorphic to the power set algebra of Λ in N. In particular if 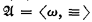 and T the theory of equality with additional axioms asserting the existence of at least n distinct elements for each n < ω, then there is an N and Λ ∈ N with 〈PN(Λ), ⊆〉 isomorphic to the countable, atomic, incomplete Boolean algebra of the finite and cofinite subsets of ω.
and T the theory of equality with additional axioms asserting the existence of at least n distinct elements for each n < ω, then there is an N and Λ ∈ N with 〈PN(Λ), ⊆〉 isomorphic to the countable, atomic, incomplete Boolean algebra of the finite and cofinite subsets of ω.
From the above we see that some incomplete Boolean algebras can be realized as power sets in standard models of ZF.
Definition 1.1. A countable Boolean algebra 〈B, ≤〉 is a pseudo-power set if there is a countable standard model of ZF, N and a set Λ ∈ N such that
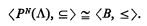
It is clear that a pseudo-power set is atomic.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1975
Footnotes
This work was partially supported by NSF grants GP-22719 and GP-38025. The authors wish to express their gratitude to Anil Nerode for numerous conversations.


