Published online by Cambridge University Press: 12 March 2014
Let B be the random real forcing. Miller [Mi] asked if there are ZFC models M ⊆ N such that forcing with BM over N adds a dominating real. A YES answer was provided by Judah and Shelah in [JS], where in a long and sophisticated construction they built such models. In this paper we prove that forcing with BV over VI, where I is the infinitely often equal real forcing of [Mi], adds a dominating real over VI. This greatly simplifies the YES answer to Miller's question. Moreover it turns out that B may be replaced here by E, the eventually different real forcing of [Mi]. This answers the second part of Miller's question. We also prove that both side by side products I × B and I × E add a Hechler dominating real over V.
In this section we establish the main result of the paper; namely, we prove that forcing over VI with either of the posets BV or EV adds a dominating real over VI.
First we recall the definitions of I and E from [Mi]. The infinitely often equal real forcing is the set
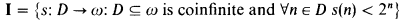
ordered by extension. Miller [Mi] proves that I is ωω bounding.