Hostname: page-component-6bf8c574d5-w79xw Total loading time: 0 Render date: 2025-02-20T06:47:12.903Z Has data issue: false hasContentIssue false
  • English
  • Français

ABELIAN GROUPS DEFINABLE IN p-ADICALLY CLOSED FIELDS

Part of: Model theory

Published online by Cambridge University Press:  18 July 2023

WILL JOHNSON Open the ORCID record for WILL JOHNSON [Opens in a new window]  and
NINGYUAN YAO
WILL JOHNSON*
Affiliation:
SCHOOL OF PHILOSOPHY FUDAN UNIVERSITY 220 HANDAN ROAD GUANGHUA WEST BUILDING ROOM 2503, SHANGHAI 200433, CHINA E-mail: [email protected] URL: http://philosophy.fudan.edu.cn/64/8b/c14253a222347/page.htm
NINGYUAN YAO
Affiliation:
SCHOOL OF PHILOSOPHY FUDAN UNIVERSITY 220 HANDAN ROAD GUANGHUA WEST BUILDING ROOM 2503, SHANGHAI 200433, CHINA E-mail: [email protected] URL: http://philosophy.fudan.edu.cn/64/8b/c14253a222347/page.htm
*
E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Recall that a group G has finitely satisfiable generics (fsg) or definable f-generics (dfg) if there is a global type p on G and a small model $M_0$ such that every left translate of p is finitely satisfiable in 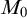$M_0$ or definable over $M_0$, respectively. We show that any abelian group definable in a p-adically closed field is an extension of a definably compact fsg definable group by a dfg definable group. We discuss an approach which might prove a similar statement for interpretable abelian groups. In the case where G is an abelian group definable in the standard model 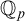$\mathbb {Q}_p$, we show that 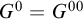$G^0 = G^{00}$, and that G is an open subgroup of an algebraic group, up to finite factors. This latter result can be seen as a rough classification of abelian definable groups in 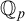$\mathbb {Q}_p$.

Keywords

definable groupsp-adically closed fieldsfinitely satisfiable generics

MSC classification

Primary: 03C60: Model-theoretic algebra
Type
Article
Information
The Journal of Symbolic Logic , First View , pp. 1 - 22
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acosta López, J. P., One dimensional groups definable in the $p$ -adic numbers, this Journal, vol. 86 (2021), no. 2, pp. 801–816.Google Scholar
Andújar Guerrero, P. and Johnson, W., Around definable types in $p$ -adically closed fields. Preprint, 2022, arXiv:2208.05815v1 [math.LO].CrossRefGoogle Scholar
Chernikov, A. and Simon, P., Definably amenable NIP groups . Journal of the American Mathematical Society , vol. 31 (2018), pp. 609–641.CrossRefGoogle Scholar
Conversano, A. and Pillay, A., Connected components of definable groups and $o$ -minimality I . Advances in Mathematics , vol. 231 (2012), pp. 605–623.CrossRefGoogle Scholar
Cubides-Kovacsics, P., Darnière, L., and Leenknegt, E., Topological cell decomposition and dimension theory in $P$ -minimal fields, this Journal, vol. 82 (2017), no. 1, pp. 347–358.Google Scholar
Gagelman, J., Stability in geometric theories . Annals of Pure and Applied Logic , vol. 132 (2005), pp. 313–326.CrossRefGoogle Scholar
Hrushovski, E., Peterzil, Y., and Pillay, A., Groups, measures, and the NIP . Journal of the American Mathematical Society , vol. 21 (2008), no. 2, pp. 563–596.CrossRefGoogle Scholar
Hrushovski, E. and Pillay, A., On NIP and invariant measures . Journal of the European Mathematical Society , vol. 13 (2011), no. 4, pp. 1005–1061.CrossRefGoogle Scholar
Johnson, W., The canonical topology on dp-minimal fields . Journal of Mathematical Logic , vol. 18 (2018), no. 2, p. 1850007.CrossRefGoogle Scholar
Johnson, W., On the proof of elimination of imaginaries in algebraically closed valued fields . Notre Dame Journal of Formal Logic , vol. 61 (2020), no. 3, pp. 363–381.CrossRefGoogle Scholar
Johnson, W., Topologizing interpretable groups in $p$ -adically closed fields. Preprint, 2022, arXiv:2205.00749v1 [math.LO].CrossRefGoogle Scholar
Johnson, W., A note on fsg groups in $p$ -adically closed fields . Mathematical Logic Quarterly , vol. 69 (2023), no. 1, pp. 50–57.CrossRefGoogle Scholar
Johnson, W. and Yao, N., On non-compact $p$ -adic definable groups, this Journal, vol. 87 (2022), no. 1, pp. 188–213.Google Scholar
Montenegro, S., Onshuus, A., and Simon, P., Stabilizers, NTP 2 groups with f-generics, and PRC fields . Journal of the Institute of Mathematics of Jussieu , no. 19 (2020), no. 3, pp. 821–853.CrossRefGoogle Scholar
Onshuus, A. and Pillay, A., Definable groups and compact $p$ -adic lie groups . Journal of the London Mathematical Society , vol. 78 (2008), no. 1, pp. 233–247.CrossRefGoogle Scholar
Peterzil, Y. and Starchenko, S., Topological groups, $\mu$ -types and their stabilizers. Journal of the European Mathematical Society , vol. 19 (2017), no. 10, pp. 2965–2995.CrossRefGoogle Scholar
Pillay, A., Type-definability, compact Lie groups, and $o$ -minimality. Journal of Mathematical Logic , vol. 4 (2004), no. 2, pp. 147–162.CrossRefGoogle Scholar
Pillay, A. and Yao, N., On minimal flows, definably amenable groups, and o-minimality . Advances in Mathematics , vol. 290 (2016), pp. 483–502.CrossRefGoogle Scholar
Pillay, A. and Yao, N., On groups with definable $f$ -generics definable in $p$ -adically closed fields. The Journal of Symbolic Logic (2023), pp. 1–20. https://doi.org/10.1017/jsl.2023.37.CrossRefGoogle Scholar
Pillay, A. and Yao, N., Open subgroups of p-adic algebraic groups. Preprint, 2023, arXiv:2304.14798v1 [math.GR].Google Scholar
Rosenlicht, M., Extensions of vector groups by abelian varieties . American Journal of Mathematics , vol. 80 (1958), no. 3, 685–714.CrossRefGoogle Scholar
Simon, P., A Guide to NIP Theories , Lecture Notes in Logic, Cambridge University Press, Cambridge, 2015.CrossRefGoogle Scholar