Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-16T21:15:35.623Z Has data issue: false hasContentIssue false
  • English
  • Français

The Σ21 theory of axioms of symmetry

Published online by Cambridge University Press:  12 March 2014

Galen Weitkamp
Galen Weitkamp*
Affiliation:
Department of Mathematics, Western Illinois University, Macomb, Illinois 61455
Get access Rights & Permissions [Opens in a new window]

Abstract

The axiom of symmetry (Aℵ0) asserts that for every function F: ω2 → ω2 there is a pair of reals x and y in ω2 so that y is not in the countable set {(F(x))n: n< ω} coded by F(x) and x is not in the set coded by F(y). A(Γ) denotes axiom Aℵ0 with the restriction that graph(F) belongs to the pointclass Γ. In §2 we prove A(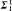). In §3 we show 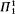A(), A(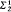) and ω2 ⊈ L are equivalent. In §4 several effective versions of A(REC) are examined.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 54 , Issue 3 , September 1989 , pp. 727 - 734
Copyright
Copyright © Association for Symbolic Logic 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Cohen, P. [1966], Set theory and the continuum hypothesis, Benjamin, New York.Google Scholar
Freiling, C. [1986], Axioms of symmetry: throwing darts at the real number line, this Journal, vol. 51, pp. 190–200.Google Scholar
Kondo, M. [1938], Sur l'uniformisation des complémentares analytiques et les ensembles projectifs de la seconde classe, Japanese Journal of Mathematics, vol. 15, pp. 197–230.CrossRefGoogle Scholar
Mansfield, R. [1970], Perfect subsets of definable sets of real numbers, Pacific Journal of Mathematics, vol. 35, pp. 451–457.CrossRefGoogle Scholar
Mansfield, R. [1975], The non-existence of Σ 21 well-orderings of the Cantor set, Fundamenta Mathematicae, vol. 86, pp. 279–282.CrossRefGoogle Scholar
Mansfield, R. and Dawson, J. [1976], Boolean-valued set theory and forcing, Synthese, vol. 33, pp. 223–252.CrossRefGoogle Scholar
Mansfield, R. and Weitkamp, G. [1985], Recursive aspects of descriptive set theory, Oxford University Press, Oxford.Google Scholar
Mycielski, J. and Świerczkowski, S. [1964], On the Lebesgue measurability and the axiom of determinateness, Fundamenta Mathematicae, vol. 54, pp. 67–71.CrossRefGoogle Scholar
Sacks, G. [1971], Forcing with perfect closed sets, Axiomatic set theory (Scott, D. S., editor), Proceedings of Symposia in Pure Mathematics, vol. 13, part 1, American Mathematical Society, Providence, Rhode Island, pp. 331–355.CrossRefGoogle Scholar
Shoenfield, J. R. [1961], The problem of predicativity, Essays on the foundations of mathematics, dedicated to A. A. Fraenkel on his seventieth anniversary (Bar-Hillel, Y. et al., editors), Magnes Press, The Hebrew University, Jerusalem, and North-Holland, Amsterdam, pp. 132–139.Google Scholar
Solovay, R. [1969], On the cardinality of Σ 21 sets of reals. Foundations of mathematics (symposium commemorating Kurt Gödel, Columbus, Ohio, 1966; Bulloff, J. J.et al., editors), Springer-Verlag, Berlin, 1969, pp. 58–73.Google Scholar
Solovay, R. [1970], A model of set-theory in which every set is Lebesgue measurable, Annals of Mathematics, ser. 2, vol. 92, pp. 1–56.CrossRefGoogle Scholar