Article contents
Σ1(κ)-DEFINABLE SUBSETS OF H(κ+)
Published online by Cambridge University Press: 08 September 2017
Abstract
We study Σ1(ω1)-definable sets (i.e., sets that are equal to the collection of all sets satisfying a certain Σ1-formula with parameter ω1 ) in the presence of large cardinals. Our results show that the existence of a Woodin cardinal and a measurable cardinal above it imply that no well-ordering of the reals is Σ1(ω1)-definable, the set of all stationary subsets of ω1 is not Σ1(ω1)-definable and the complement of every Σ1(ω1)-definable Bernstein subset of 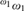 ${}_{}^{{\omega _1}}\omega _1^{}$ is not Σ1(ω1)-definable. In contrast, we show that the existence of a Woodin cardinal is compatible with the existence of a Σ1(ω1)-definable well-ordering of H(ω2) and the existence of a Δ1(ω1)-definable Bernstein subset of
${}_{}^{{\omega _1}}\omega _1^{}$ is not Σ1(ω1)-definable. In contrast, we show that the existence of a Woodin cardinal is compatible with the existence of a Σ1(ω1)-definable well-ordering of H(ω2) and the existence of a Δ1(ω1)-definable Bernstein subset of 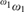 ${}_{}^{{\omega _1}}\omega _1^{}$. We also show that, if there are infinitely many Woodin cardinals and a measurable cardinal above them, then there is no Σ1(ω1)-definable uniformization of the club filter on ω1. Moreover, we prove a perfect set theorem for Σ1(ω1)-definable subsets of
${}_{}^{{\omega _1}}\omega _1^{}$. We also show that, if there are infinitely many Woodin cardinals and a measurable cardinal above them, then there is no Σ1(ω1)-definable uniformization of the club filter on ω1. Moreover, we prove a perfect set theorem for Σ1(ω1)-definable subsets of 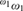 ${}_{}^{{\omega _1}}\omega _1^{}$, assuming that there is a measurable cardinal and the nonstationary ideal on ω1 is saturated. The proofs of these results use iterated generic ultrapowers and Woodin’s ℙmax-forcing. Finally, we also prove variants of some of these results for Σ1(κ)-definable subsets of κκ, in the case where κ itself has certain large cardinal properties.
${}_{}^{{\omega _1}}\omega _1^{}$, assuming that there is a measurable cardinal and the nonstationary ideal on ω1 is saturated. The proofs of these results use iterated generic ultrapowers and Woodin’s ℙmax-forcing. Finally, we also prove variants of some of these results for Σ1(κ)-definable subsets of κκ, in the case where κ itself has certain large cardinal properties.
Keywords
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2017
References
REFERENCES
- 4
- Cited by


