Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-01-11T21:54:12.791Z Has data issue: false hasContentIssue false
  • English
  • Français

Σ1-compactness in languages stronger than

Published online by Cambridge University Press:  12 March 2014

Nigel Cutland
Nigel Cutland*
Affiliation:
University of Hull, N. Humberside, England
Get access Rights & Permissions [Opens in a new window]

Extract

One of the main results of Barwise [2] (see also [7, Chapter VIII]) showed that the s – 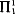reflection principle for a set A is equivalent to Σ1-compactness of 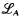. Here A is any transitive p.r. closed set, and 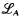is the infinitary language on A which allows conjunction and disjunction over arbitrary sets Φ Є A, and finite quantification.

In this paper we consider languages 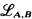, where B is a Δ0 subset of A, which is like 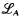but we allow quantifiers ∀x and ∃x where x is any set of variables indexed by an element of B. A treatment similar to that of [2] for 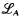establishes a sufficient, and in some cases necessary, condition for 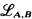to be Σ1-compact. The use of infinitary Skolem functions is intrinsic to the method, so to avoid a separate development of the rudiments of the Skolem language we actually define 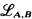to have b-ary relation and function symbols for every b Є B.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 43 , Issue 3 , September 1978 , pp. 508 - 520
Copyright
Copyright © Association for Symbolic Logic 1978

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Barwise, J., Implicit definability and compactness in infinitary languages, The syntax and semantics of infinitary languages, Lecture Notes in Mathematics, vol. 72 (1968), Springer-Verlag, Berlin and New York, pp. 1–35.CrossRefGoogle Scholar
[2]Barwise, J., Applications of strict Π11-predicates to infinitary logic, this Journal, vol. 34 (1969), pp. 409–423.Google Scholar
[3]Barwise, J., Gandy, R. O. and Moschovakis, Y., The next admissible set, this Journal, vol. 36 (1971), pp. 108–120.Google Scholar
[4]Chang, C. C., Sets constructible using Lκκ, Axiomatic set theory, Proceedings of Symposia in Pure Mathematics, vol. 13 (1971), Part I, American Mathematical Society, pp. 1–8.Google Scholar
[5]Jensen, R. and Karp, C., Primitive recursive set functions, Axiomatic set theory, Proceedings of Symposia in Pure Mathematics, vol. 13 (1971), Part I, American Mathematical Society, pp. 143–176.CrossRefGoogle Scholar
[6]Stark, W. R., Compactness and completeness for large languages (to appear).Google Scholar
[7]Barwise, J., Admissible sets and structures, Springer-Verlag, Berlin and New York, 1975.CrossRefGoogle Scholar