Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-24T12:09:19.120Z Has data issue: false hasContentIssue false
  • English
  • Français

Π11 relations and paths through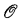

Published online by Cambridge University Press:  12 March 2014

Sergey S. Goncharov ,
Valentina S. Harizanov ,
Julia F. Knight  and
Richard A. Shore
Sergey S. Goncharov
Affiliation:
Academy of Sciences, Siberian Branch, Mathematical Institute, 630090 Novosibirsk, Russia, E-mail: [email protected]
Valentina S. Harizanov
Affiliation:
Department of Mathematics, The George Washington University, Washington, DC. 20052, U.S.A., E-mail: [email protected]
Julia F. Knight
Affiliation:
Department of Mathematics, University of Notre Dame, Notre Dame, IN 46556, U.S.A., E-mail: [email protected]
Richard A. Shore
Affiliation:
Department of Mathematics, Cornell University, Ithaca, NY 14853, U.S.A., E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

When bounds on complexity of some aspect of a structure are preserved under isomorphism, we refer to them as intrinsic. Here, building on work of Soskov [34], [33], we give syntactical conditions necessary and sufficient for a relation to be intrinsically 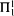on a structure. We consider some examples of computable structures 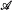and intrinsically 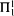relations R. We also consider a general family of examples of intrinsically 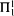relations arising in computable structures of maximum Scott rank.

For three of the examples, the maximal well-ordered initial segment in a Harrison ordering, the superatomic part of a Harrison Boolean algebra, and the height-possessing part of a Harrison p-group, we show that the Turing degrees of images of the relation in computable copies of the structure are the same as the Turing degrees of 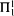paths through Kleene's 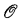. With this as motivation, we investigate the possible degrees of these paths. We show that there is a 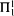path in which ∅′ is not computable. In fact, there is one in which no noncomputable hyperarithmetical set is computable. There are paths that are Turing incomparable, or Turing incomparable over a given hyperarithmetical set. There is a pair of paths whose degrees form a minimal pair. However, there is no path of minimal degree.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 69 , Issue 2 , June 2004 , pp. 585 - 611
Copyright
Copyright © Association for Symbolic Logic 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Ash, C. J. and Knight, J. F., Possible degrees in recursive copies, Annals of Pure and Applied Logic, vol. 75 (1995), pp. 215–221.CrossRefGoogle Scholar
[2]Ash, C. J. and Knight, J. F., Possible degrees in recursive copies II, Annals of Pure and Applied Logic, vol. 87 (1997), pp. 151–165.CrossRefGoogle Scholar
[3]Ash, C. J. and Knight, J. F., Computable structures and the hyperarithmetical hierarchy, Elsevier, 2000.Google Scholar
[4]Ash, C. J., Knight, J. F., Manasse, M., and Slaman, T., Generic copies of countable structures, Annals of Pure and Applied Logic, vol. 42 (1989), pp. 195–205.CrossRefGoogle Scholar
[5]Ash, C. J. and Nerode, A., Intrinsically recursive relations, Aspects of effective algebra (Crossley, J. N., editor), Steel's Creek, Australia, Upside Down A Book Co., 1981, pp. 26–41.Google Scholar
[6]Barker, E., Intrinsically relations, Annals of Pure and Applied Logic, vol. 39 (1988), pp. 105–130.CrossRefGoogle Scholar
[7]Barwise, J., Infinitary logic and admissible sets, this Journal, vol. 34 (1969), pp. 226–252.Google Scholar
[8]Chisholm, J., Effective model theory vs. recursive model theory, this Journal, vol. 55 (1990), pp. 1168–1191.Google Scholar
[9]Downey, R., Jockusch, C. G. Jr., and Stob, M., Array nonrecursive degrees and genericity, Computability, enumerability, unsolvability, London Mathematical Society Lecture Notes Series, vol. 224, Cambridge University Press, 1996, pp. 93–104.CrossRefGoogle Scholar
[10]Friedman, H., One hundred and two problems in mathematical logic, this Journal, vol. 40 (1975), pp. 113–129.Google Scholar
[11]Friedman, H., Recursiveness in paths through , Proceedings of the American Mathematical Society, vol. 54 (1976), pp. 311–315.Google Scholar
[12]Goncharov, S. S., The quantity of nonautoequivalent constructivizations, Algebra and Logic, vol. 16 (1977), pp. 169–185, English translation.CrossRefGoogle Scholar
[13]Goncharov, S. S., Harizanov, V. S., Knight, J. F., McCoy, C., Miller, R. G., and Solomon, R., Enumerations in computable structure theory, submited.Google Scholar
[14]Goncharov, S. S. and Knight, J. F., Computable structure and non-structure theorems, Algebra and Logic, vol. 41 (2002), pp. 351–373, English translation.CrossRefGoogle Scholar
[15]Harizanov, V. S., Some effects of Ash-Nerode and other decidability conditions on degree spectra, Annals of Pure and Applied Logic, vol. 55 (1991), pp. 51–65.CrossRefGoogle Scholar
[16]Harrington, L., McLaughlin's conjecture, handwritten notes, 1976.Google Scholar
[17]Harrison, J., Recursive pseudo-well-orderings, Transactions of the American Mathematical Society, vol. 131 (1968), pp. 526–543.CrossRefGoogle Scholar
[18]Hirschfeldt, D. R., Khoussainov, B., Shore, R. A., and Slinko, A. M., Degree spectra and computable dimensions in algebraic structures, Annals of Pure and Applied Logic, vol. 115 (2002), pp. 71–113.CrossRefGoogle Scholar
[19]Jockusch, C. G. Jr., Recursiveness of initial segments of Kleene's , Fundamenta Mathematical vol. 87 (1975), pp. 161–167.CrossRefGoogle Scholar
[20]Jockusch, C. G. Jr., and McLaughlin, T. G., Countable retracing functions and predicates, Pacific Journal of Mathematics, vol. 30 (1969), pp. 67–93.CrossRefGoogle Scholar
[21]Kaplansky, I., Infinite abelian groups, University of Michigan Press, 1954.Google Scholar
[22]Khousainov, B. and Shore, R. A., Computable isomorphisms, degree spectra of relations and Scott families, Annals of Pure and Applied Logic, vol. 93 (1998), pp. 153–193.CrossRefGoogle Scholar
[23]Kreisel, G., Set theoretic problems suggested by the notion of potential totality, Infinitistic methods, Proceedings of the Symposium on Foundations of Mathematics, Warsaw, 1959, Pergamon, 1961, pp. 103–140.Google Scholar
[24]Lachlan, A. H., Solution to a problem of Spector, Canadian Journal of Mathematics, vol. 23 (1971), pp. 247–256.CrossRefGoogle Scholar
[25]Lerman, M., Degrees of unsolvability, Springer-Verlag, Berlin, 1983.CrossRefGoogle Scholar
[26]Manasse, M. S., Techniques and counterexamples in almost categorical recursive model theory, Ph.D. thesis, University of Wisconsin-Madison, 1982.Google Scholar
[27]Parikh, R., A note on paths through , Proceedings of the American Mathematical Society, vol. 39 (1973), pp. 178–180.Google Scholar
[28]Ressayre, J. P., Models with compactness properties relative to an admissible language, Annals of Mathematical Logic, vol. 11 (1977), pp. 31–55.CrossRefGoogle Scholar
[29]Rogers, H. Jr., Theory of recursive functions and effective computability, McGraw-Hill, New York, 1967.Google Scholar
[30]Sacks, G. E., On the number of countable models, Southeast Asian Conference on Logic (Singapore, 1981) (Chong, C. T. and Wicks, M. J., editors), North-Holland, 1983, pp. 185–195.CrossRefGoogle Scholar
[31]Sacks, G. E., Higher recursion theory, Springer-Verlag, 1990.CrossRefGoogle Scholar
[32]Scott, D., Logic with denumerably long formulas and finite strings of quantifiers, The theory of models (Addison, J. W., Henkin, L., and Tarski, A., editors), Proc. 1963 Internat. Sympos. Berkeley, North-Holland, 1965, pp. 329–341.Google Scholar
[33]Soskov, I. N., Intrinsically hyperarithmetical sets, Mathematical Logic Quarterly, vol. 42 (1996), pp. 469–480.CrossRefGoogle Scholar
[34]Soskov, I. N., Intrinsically relations, Mathematical Logic Quarterly, vol. 42 (1996), pp. 109–126.CrossRefGoogle Scholar
[35]Spector, C., Recursive well-orderings, this Journal, vol, 20 (1955), pp. 151–163.Google Scholar
[36]Steel, J. R., Forcing with tagged trees, Annals of Mathematical Logic, vol. 15 (1978), pp. 55–74.CrossRefGoogle Scholar