Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-10T02:38:46.336Z Has data issue: false hasContentIssue false
  • English
  • Français

Π11 Borel sets

Published online by Cambridge University Press:  12 March 2014

Alexander S. Kechris ,
David Marker  and
Ramez L. Sami
Alexander S. Kechris
Affiliation:
Department of Mathematics, California Institute of Technology, Pasadena, California 91125 Department of Mathematics, Statistics, and Computer Science, University of Illinois at Chicago, Chicago, Illinois 60680
David Marker
Affiliation:
Department of Mathematics, Cairo University, Cairo, Egypt
Ramez L. Sami
Affiliation:
UER de Mathématique, Université Paris-VII, 75251 Paris, France
Get access Rights & Permissions [Opens in a new window]

Extract

The results in this paper were motivated by the following question of Sacks. Suppose T is a recursive theory with countably many countable models. What can you say about the least ordinal α such that all models of T have Scott rank below α? If Martin's conjecture is true for T then α ≤ ω · 2.

Our goal was to look at this problem in a more abstract setting. Let E be a 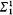equivalence relation on ωω with countably many classes each of which is Borel. What can you say about the least α such that each equivalence class is 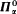? This problem is closely related to the following question. Suppose X ⊆ ωω is 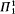and Borel. What can you say about the least α such that X is ?

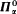In §1 we answer these questions in ZFC. In §2 we give more informative answers under the added assumptions V = L or 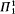-determinacy. The final section contains related results on the separation of 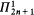sets by Borel sets.

Our notation is standard. The reader may consult Moschovakis [5] for undefined terms.

Some of these results were proved first by Sami and rediscovered by Kechris and Marker.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 54 , Issue 3 , September 1989 , pp. 915 - 920
Copyright
Copyright © Association for Symbolic Logic 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Kechris, A. S., Countable ordinals and the analytical hierarchy. I, Pacific Journal of Mathematics, vol. 60 (1975), pp. 223–227.CrossRefGoogle Scholar
[2]Kechris, A. S. and Moschovakis, Y., Two theorems about projective sets, Israel Journal of Mathematics, vol. 12 (1972), pp. 391–399.CrossRefGoogle Scholar
[3]Louveau, A., A separation theorem for Π11 sets, Transactions of the American Mathematical Society, vol. 260(1980), pp. 363–378.Google Scholar
[4]Louveau, A. and Raymond, J. Saint, Borel classes and closed games: Wadge-type and Hurewicz-type results, Transactions of the American Mathematical Society, vol. 304 (1987), pp. 431–467.CrossRefGoogle Scholar
[5]Moschovakis, Y., Descriptive set theory, North-Holland, Amsterdam, 1980.Google Scholar
[6]Sami, R., On Σ 11 equivalence relations with Borel classes of bounded rank, this Journal, vol. 49 (1984), pp. 1273–1283.Google Scholar
[7]Sami, R., Polish group actions and the Vaught conjecture (preprint).Google Scholar
[8]Steel, J., Determinateness and the separation property, this Journal, vol. 46 (1981), pp. 41–44.Google Scholar
[9]Stern, J., Evaluation du rang de Borel de certains ensembles (preprint).Google Scholar
[10]Sami, R., On Lusin's restricted continuum problem (preprint).Google Scholar