Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-24T18:54:35.207Z Has data issue: false hasContentIssue false
  • English
  • Français

ℵ0-categorical structures with arbitrarily fast growth of algebraic closure

Published online by Cambridge University Press:  12 March 2014

David M. Evans  and
M. E. Pantano
David M. Evans
Affiliation:
School of Mathematics, University of East Anglia, Norwich NR4 7TJ, England, E-mail: [email protected]
M. E. Pantano
Affiliation:
School of Mathematics, University of East Anglia, Norwich NR4 7TJ, England
Get access Rights & Permissions [Opens in a new window]

Extract

Various results have been proved about growth rates of certain sequences of integers associated with infinite permutation groups. Most of these concern the number of orbits of the automorphism group of an ℵ0-categorical structure 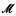on the set of unordered n-subsets or on the set of n-tuples of elements of 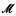. (Recall that by the Ryll-Nardzewski Theorem, if 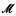is countable and ℵ0-categorical, the number of the orbits of its automorphism group Aut(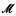) on the set of n-tuples from 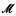is finite and equals the number of complete n-types consistent with the theory of 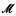.) The book [Ca90] is a convenient reference for these results. One of the oldest (in the realms of ‘folklore’) is that for any sequence (Kn)n∈ℕ of natural numbers there is a countable ℵ0-categorical structure 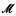such that the number of orbits of Aut(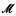) on the set of n-tuples from 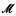is greater than kn for all n.

These investigations suggested the study of the growth rate of another sequence. Let 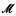be an ℵ0-categorical structure and X be a finite subset of 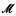. Let acl(X) be the algebraic closure of X, that is, the union of the finite X-definable subsets of 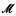. Equivalently, this is the union of the finite orbits on 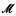of Aut(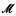)(X), the pointwise stabiliser of X in Aut(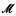). Define

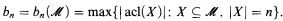
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 67 , Issue 3 , September 2002 , pp. 897 - 909
Copyright
Copyright © Association for Symbolic Logic 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[Ca90]Cameron, P.J., Oligomorphic permutation groups, Cambridge University Press, Cambridge, 1990.CrossRefGoogle Scholar
[CK90]Chang, C. C. and Keisler, H.J., Model theory, third ed., North-Holland, Amsterdam, 1990.Google Scholar
[CHL85]Cherlin, G., Harrington, L., and Lachlan, A.H., ℵ0-categorical, ℵ0-stable structures, Annals of Pure and Applied Logic, vol. 28 (1985), pp. 1030–135.CrossRefGoogle Scholar
[Ev94]Evans, David M., Examples of ℵ0-categorical structures, Automorphisms of first-order structures (Kaye, R. and Macpherson, D., editors), Oxford University Press, Oxford, 1994.Google Scholar
[Ev00]Evans, David M., ℵ0-categorical structures with apredimension, to appear in Annals of Pure and Applied Logic, (2000), Preprint.Google Scholar
[Fr53]Fraïssé, R., Sur certains relations qui généralised l'ordre des nombres rationnels, Comptes Rendus de l'Académie des Sciences, Paris, vol. 237 (1953), pp. 540–542.Google Scholar
[Fr54]Fraïssé, R., Sur l'extension aux relations de quelques propriétés des ordres, Annates Scientifiques de l'École Normale Supérieure, vol. 71 (1954), pp. 363–388.CrossRefGoogle Scholar
[Ho93]Hodges, W., Model theory, Cambridge University Press, Cambridge, 1993.CrossRefGoogle Scholar
[Hr88]Hrushovski, Ehud, A stable ℵ0-categorical pseudoplane, Unpublished notes, 1988.Google Scholar
[Hr93]Hrushovski, Ehud, A new strongly minimal set, Annals of Pure and Applied Logic, vol. 62 (1993), pp. 147–166.CrossRefGoogle Scholar
[Hr97]Hrushovski, Ehud, Simplicity and the Lascar group, Preprint, 1997.Google Scholar
[KL92]Kueker, D. W. and Laskowski, M.C., On generic structures, Notre Dame Journal of Formal Logic, vol. 33 (1992), pp. 175–183.CrossRefGoogle Scholar
[Ma86]Macpherson, H.D., Groups of automorphisms of ℵ0-categorical structures, Quarterly Journal of Mathematics. Oxford, vol. 37 (1986), pp. 449–465.CrossRefGoogle Scholar
[Pa95]Pantano, M.E., Algebraic closure in ℵ0-categorical structures, Ph.D. thesis, University of East Anglia, Norwich, 1995.Google Scholar
[St92]Steitz, P.W., Upper bounds for growth in the Ryll-Nardzewski function of an ω-categorical, ω-stable theory, Israel Journal of Mathematics, vol. 77 (1992), pp. 335–343.CrossRefGoogle Scholar
[Wa94]Wagner, F.O., Relational structures and dimensions, Automorphisms of first-order structures (Kaye, R. and Macpherson, D., editors), Oxford University Press, Oxford, 1994.Google Scholar