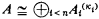Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Baur, Walter
1976.
Undecidability of the theory of abelian groups with a subgroup.
Proceedings of the American Mathematical Society,
Vol. 55,
Issue. 1,
p.
125.
Cherlin, Gregory
and
Rosenstein, Joseph G.
1978.
On ℵ 0-categorical Abelian by finite groups.
Journal of Algebra,
Vol. 53,
Issue. 1,
p.
188.
Baur, Walter
Cherlin, Gregory
and
Macintyre, Angus
1979.
Totally categorical groups and rings.
Journal of Algebra,
Vol. 57,
Issue. 2,
p.
407.
Hodges, Wilfrid
1981.
Encoding orders and trees in binary relations.
Mathematika,
Vol. 28,
Issue. 1,
p.
67.
Baldwin, John T.
and
McKenzie, Ralph N.
1982.
Counting models in universal Horn classes.
Algebra Universalis,
Vol. 15,
Issue. 1,
p.
359.
Markov, V. T.
Mikhalev, A. V.
Skornyakov, L. A.
and
Tuganbaev, A. A.
1983.
Modules.
Journal of Soviet Mathematics,
Vol. 23,
Issue. 6,
p.
2642.
Apps, A.B
1983.
On ℵ0-categorical class two groups.
Journal of Algebra,
Vol. 82,
Issue. 2,
p.
516.
Tulipani, Sauro
1983.
On the size of congruence lattices for models of theories with definability of congruences.
Algebra Universalis,
Vol. 17,
Issue. 1,
p.
346.
Prest, Mike
1984.
Rings of finite representation type and modules of finite Morley rank.
Journal of Algebra,
Vol. 88,
Issue. 2,
p.
502.
Ziegler, Martin
1984.
Model theory of modules.
Annals of Pure and Applied Logic,
Vol. 26,
Issue. 2,
p.
149.
Kremer, E. M.
1985.
Modules with an almost categorical theory.
Siberian Mathematical Journal,
Vol. 25,
Issue. 6,
p.
888.
Cherlin, Gregory
1986.
Logic, Methodology and Philosophy of Science VII, Proceedings of the Seventh International Congress of Logic, Methodology and Philosophy of Science.
Vol. 114,
Issue. ,
p.
99.
Hart, Bradd
Starchenko, Sergei
and
Valeriote, Matthew
1994.
Vaught’s conjecture for varieties.
Transactions of the American Mathematical Society,
Vol. 342,
Issue. 1,
p.
173.
Ivanov, A.
and
Majcher, K.
2007.
Ages of Expansions of ω-Categorical Structures.
Notre Dame Journal of Formal Logic,
Vol. 48,
Issue. 3,
Ivanov, Aleksander
2010.
On ω-categorical groups and their completions.
Journal of Group Theory,
Vol. 13,
Issue. 2,
Kulpeshov, Beibut Shaiykovich
Pavlyuk, Inessa Ivanovna
and
Sudoplatov, Sergey Vladimirovich
2025.
Псевдо-счетно-категоричные формулы и теории.
Математические заметки,
Vol. 117,
Issue. 3,
p.
422.